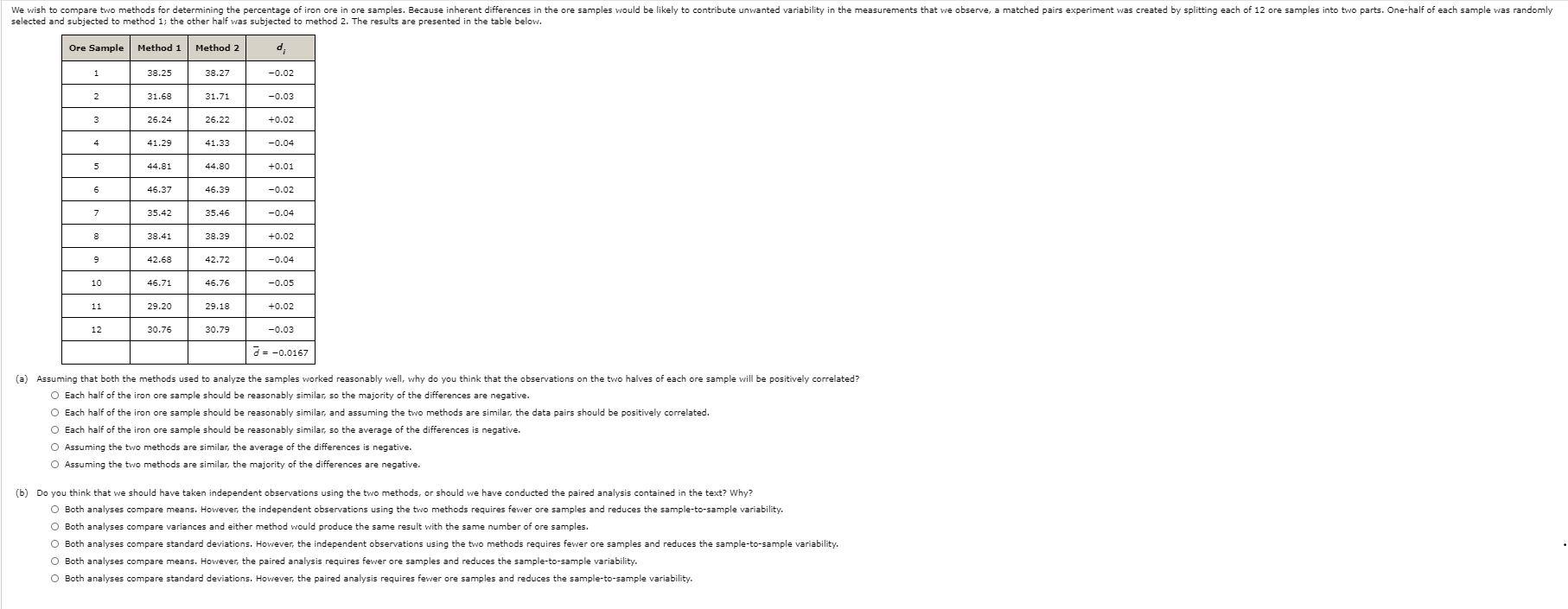
Question: We wish to compare two methods for determining the percentage of iron ore in ore samples. Because inherent differences in the ore samples would be
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


