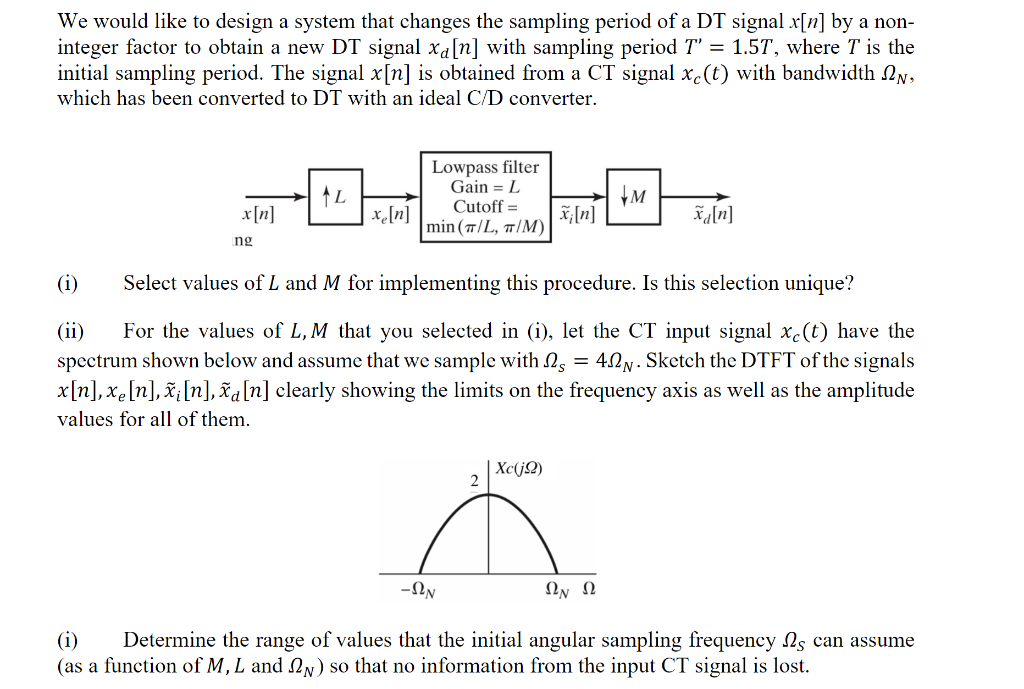
We would like to design a system that changes the sampling period of a DT signal x[n] by a non- integer factor to obtain a new DT signal xa[n] with sampling period T' = 1.57, where T is the initial sampling period. The signal x[n] is obtained from a CT signal xc(t) with bandwidth 2n, which has been converted to DT with an ideal C/D converter. AL Lowpass filter Gain = L Cutoff = min(TIL, /M) M x[n] x[n] Xa[n] ng Select values of L and M for implementing this procedure. Is this selection unique? (ii) For the values of L, M that you selected in (i), let the CT input signal xc(t) have the spectrum shown below and assume that we sample with Ns = 4.1n. Sketch the DTFT of the signals x[n], xe [n], ; [n], a[n] clearly showing the limits on the frequency axis as well as the amplitude values for all of them. Xc(2) 2 -12 12 Determine the range of values that the initial angular sampling frequency Is can assume (as a function of M, L and 2n) so that no information from the input CT signal is lost. We would like to design a system that changes the sampling period of a DT signal x[n] by a non- integer factor to obtain a new DT signal xa[n] with sampling period T' = 1.57, where T is the initial sampling period. The signal x[n] is obtained from a CT signal xc(t) with bandwidth 2n, which has been converted to DT with an ideal C/D converter. AL Lowpass filter Gain = L Cutoff = min(TIL, /M) M x[n] x[n] Xa[n] ng Select values of L and M for implementing this procedure. Is this selection unique? (ii) For the values of L, M that you selected in (i), let the CT input signal xc(t) have the spectrum shown below and assume that we sample with Ns = 4.1n. Sketch the DTFT of the signals x[n], xe [n], ; [n], a[n] clearly showing the limits on the frequency axis as well as the amplitude values for all of them. Xc(2) 2 -12 12 Determine the range of values that the initial angular sampling frequency Is can assume (as a function of M, L and 2n) so that no information from the input CT signal is lost