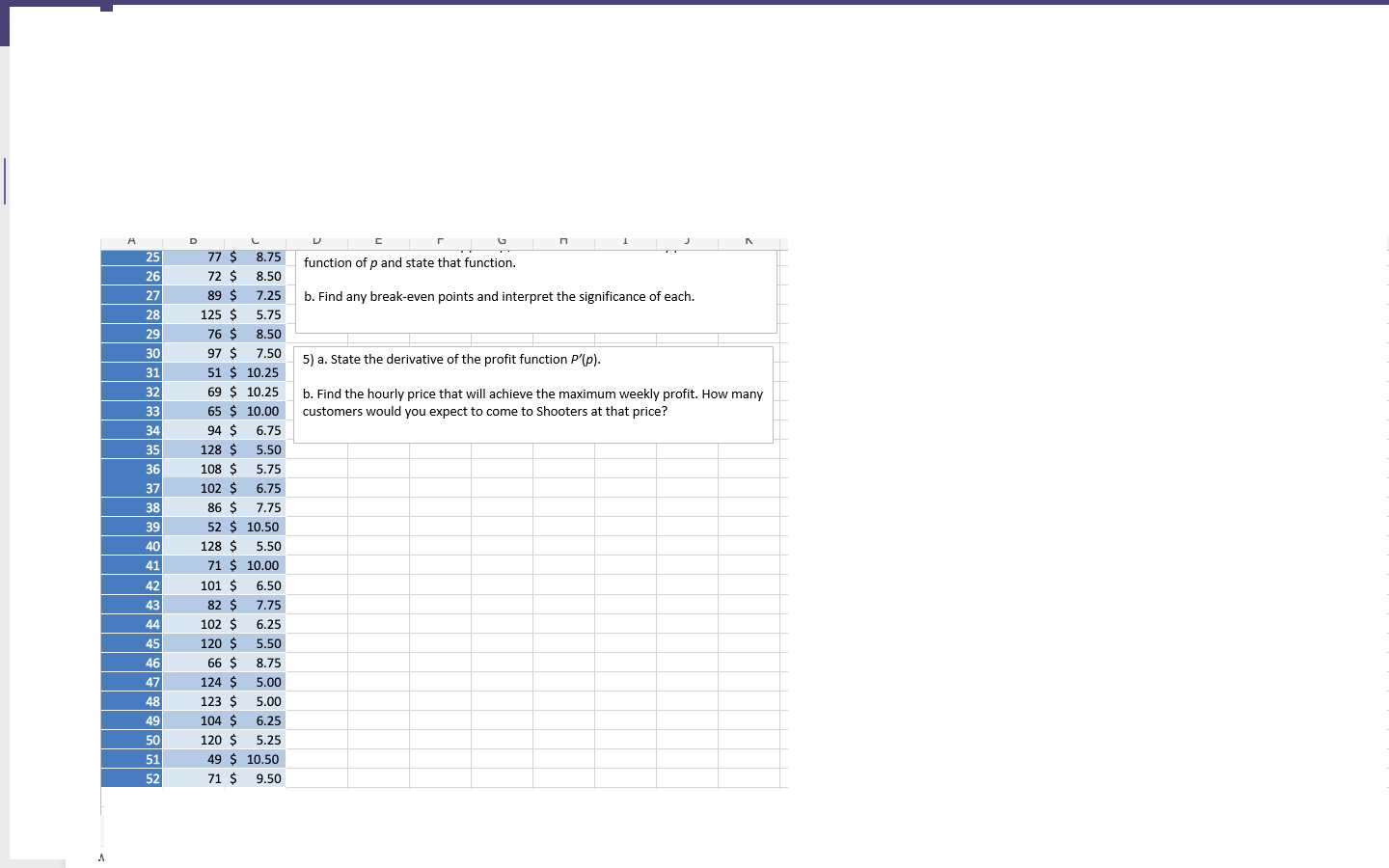
Week 1) The data below represents the managers record over the past year. For each week during the year, he recorded the price it would cost to play pool for 1 hour and the average number of hourly patrons during that week. Use this data to create a graph and determine the weekly demand d as an exponential function of the hourly price p and state that function. 2) Based on day-to-day operations, the manager has determined that he would like to predict the number of customers he can serve according to the relationship s = 20p0.65 where p is the hourly supply price. What price and quantity would result in Shooters reaching a market equilibrium? Explain how you found those values. People, d Price, 56 $ 10.25 2 68 $ 9.00 3 81 $ 8.50 4 69 $ 8.50 5 117 $ 6.00 6 69 $ 10.25 7 46 $ 10.75 8 105 $ 6.25 9 63 $ 10.50 10 114 $ 5.75 11 74 $ 8.00 12 88 $ 7.75 13 121 $ 6.00 14 109 $ 5.75 15 66 $ 9.00 16 95 $ 7.50 17 60 $ 10.50 18 88 $ 8.25 19 114 $ 6.25 20 67 $ 10.00 21 79 $ 8.00 22 88 $ 7.75 23 90 $ 7.00 24 71 $ 9.75 25 77 $ 8.75 26 72 $ 8.50 27 89 $ 7.25 28 125 $ 5.75 3) In addition to finding the equilibrium, the manager would like to determine the weekly cost, revenue and profit. a. State the revenue R as a function of the hourly price p and state its derivative. b. What price must the manager charge to achieve maximum revenue? What is the maximum revenue? Explain how you found these values. 4) The manager has estimated that the weekly expenses are about $250 plus about $1.25 per customer. a. Determine the weekly cost C as a function of the number of patrons q. State that function. Combine this with the demand equation to state the weekly cost Cas a function of the hourly price p, then determine the weekly profit as a function of p and state that function. b. Find any break-even points and interpret the significance of each. function of p and state that function. 25 26 27 28 b. Find any break-even points and interpret the significance of each. 5) a. State the derivative of the profit function P'p). 29 30 31 32 33 34 b. Find the hourly price that will achieve the maximum weekly profit. How many customers would you expect to come to Shooters at that price? 35 36 37 38 39 77 $ 8.75 72 $ 8.50 89 $ 7.25 125 $ 5.75 76 $ 8.50 97 $ 7.50 51 $ 10.25 69 $ 10.25 65 $ 10.00 94 $ 6.75 128 $ 5.50 108 $ 5.75 102 $ 6.75 86 $ 7.75 52 $ 10.50 128 $ 5.50 71 $ 10.00 101 $ 6.50 82 $ 102 $ 6.25 120 $ 5.50 66 $ 8.75 124 $ 5.00 123 $ 5.00 104 $ 6.25 120 $ 5.25 49 $ 10.50 71 $ 9.50 40 41 42 43 7.75 44 45 46 47 48 49 50 51 52 Week 1) The data below represents the managers record over the past year. For each week during the year, he recorded the price it would cost to play pool for 1 hour and the average number of hourly patrons during that week. Use this data to create a graph and determine the weekly demand d as an exponential function of the hourly price p and state that function. 2) Based on day-to-day operations, the manager has determined that he would like to predict the number of customers he can serve according to the relationship s = 20p0.65 where p is the hourly supply price. What price and quantity would result in Shooters reaching a market equilibrium? Explain how you found those values. People, d Price, 56 $ 10.25 2 68 $ 9.00 3 81 $ 8.50 4 69 $ 8.50 5 117 $ 6.00 6 69 $ 10.25 7 46 $ 10.75 8 105 $ 6.25 9 63 $ 10.50 10 114 $ 5.75 11 74 $ 8.00 12 88 $ 7.75 13 121 $ 6.00 14 109 $ 5.75 15 66 $ 9.00 16 95 $ 7.50 17 60 $ 10.50 18 88 $ 8.25 19 114 $ 6.25 20 67 $ 10.00 21 79 $ 8.00 22 88 $ 7.75 23 90 $ 7.00 24 71 $ 9.75 25 77 $ 8.75 26 72 $ 8.50 27 89 $ 7.25 28 125 $ 5.75 3) In addition to finding the equilibrium, the manager would like to determine the weekly cost, revenue and profit. a. State the revenue R as a function of the hourly price p and state its derivative. b. What price must the manager charge to achieve maximum revenue? What is the maximum revenue? Explain how you found these values. 4) The manager has estimated that the weekly expenses are about $250 plus about $1.25 per customer. a. Determine the weekly cost C as a function of the number of patrons q. State that function. Combine this with the demand equation to state the weekly cost Cas a function of the hourly price p, then determine the weekly profit as a function of p and state that function. b. Find any break-even points and interpret the significance of each. function of p and state that function. 25 26 27 28 b. Find any break-even points and interpret the significance of each. 5) a. State the derivative of the profit function P'p). 29 30 31 32 33 34 b. Find the hourly price that will achieve the maximum weekly profit. How many customers would you expect to come to Shooters at that price? 35 36 37 38 39 77 $ 8.75 72 $ 8.50 89 $ 7.25 125 $ 5.75 76 $ 8.50 97 $ 7.50 51 $ 10.25 69 $ 10.25 65 $ 10.00 94 $ 6.75 128 $ 5.50 108 $ 5.75 102 $ 6.75 86 $ 7.75 52 $ 10.50 128 $ 5.50 71 $ 10.00 101 $ 6.50 82 $ 102 $ 6.25 120 $ 5.50 66 $ 8.75 124 $ 5.00 123 $ 5.00 104 $ 6.25 120 $ 5.25 49 $ 10.50 71 $ 9.50 40 41 42 43 7.75 44 45 46 47 48 49 50 51 52