Question: Week 5 Consider the functions f ( x , y , z ) = x + 3 y + 2 z , and , g
Week
Consider the functions
and
Write down the gradients gradf and gradg.
Use the method Lagrange multipliers find the minimum value the function
the implicitly defined surface
Consider the function
Find the gradient vector gradf and the Hessian matrix
has exactly one stationary point. Find showing your working.
this stationary point a local minimum, a local maximum, a saddle point? Explain why.
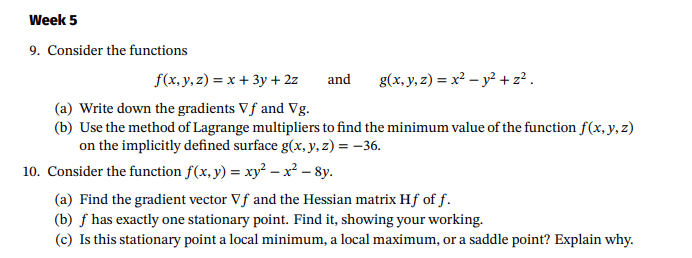
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


