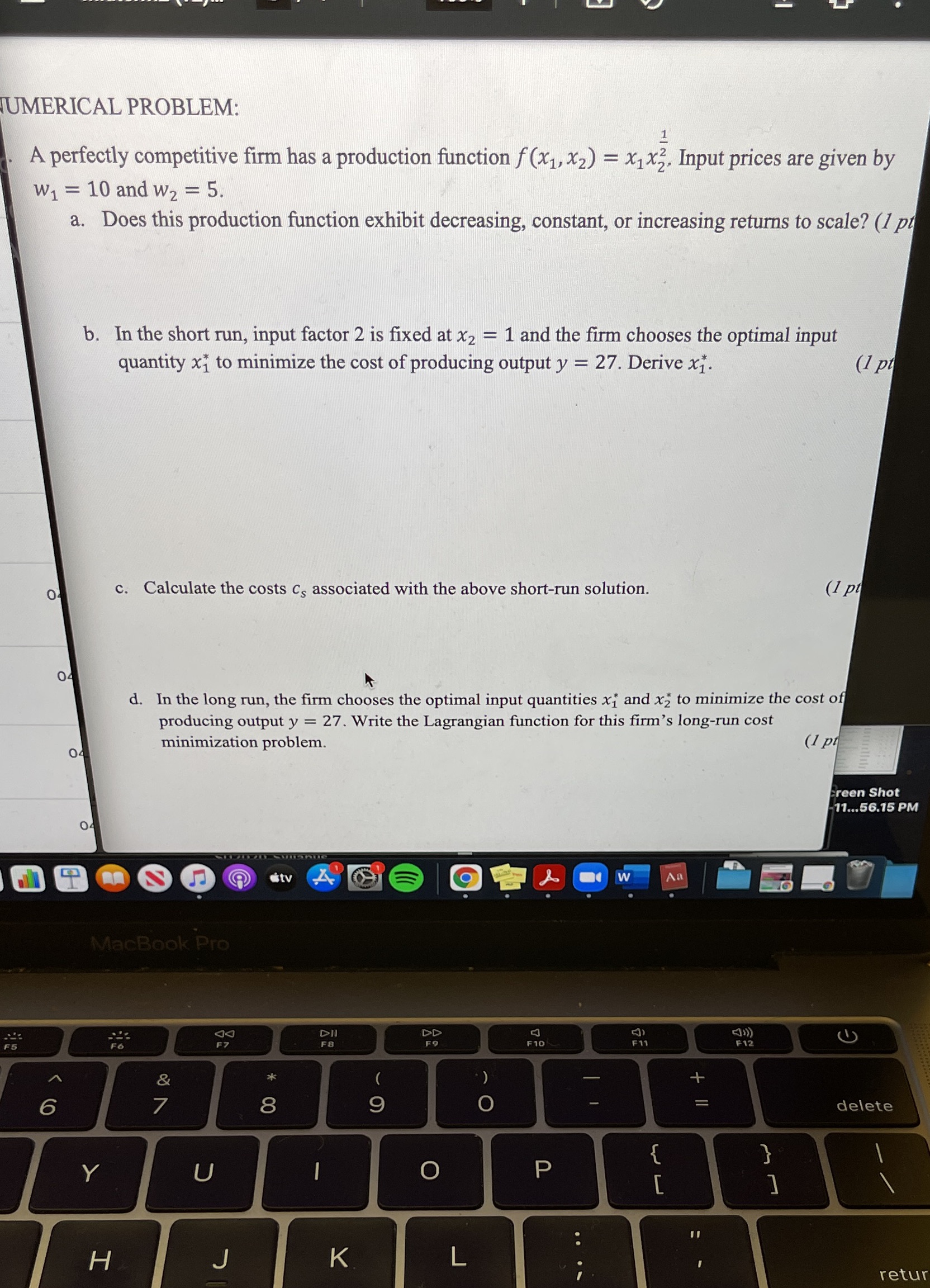
WERICAL PROBLEM: l ,. A perfectly competitive rm has a production function f (x1, x2) = xlxz, Input prices are given by w1 = 10 andwz = 5. a. Does this production function exhibit decreasing, constant, or increasing returns to scale? (1p ' "(ref-5231': ' i; b. In the short run, input factor 2 is xed at x2 = 1 and the rm chooses the optimal input quantity x; to minimize the cost of producing output y = 27. Derive xf. (1p i _-, i .1:- .~ 1: W; i 1. l ; i I i l \" 0 i' 1' c. Calculate the costs Cs associated with the above short-run solution. (1}? i I: i . i I.. 0 i ;_ k d. In the long run, the rm chooses the optimal input quantities x; and x; to minimize the cost 0 producing output 31 = 27. Write the Lagrangian mction for this rm's long-run cost minimization problem. men Shot H...56.15 PM