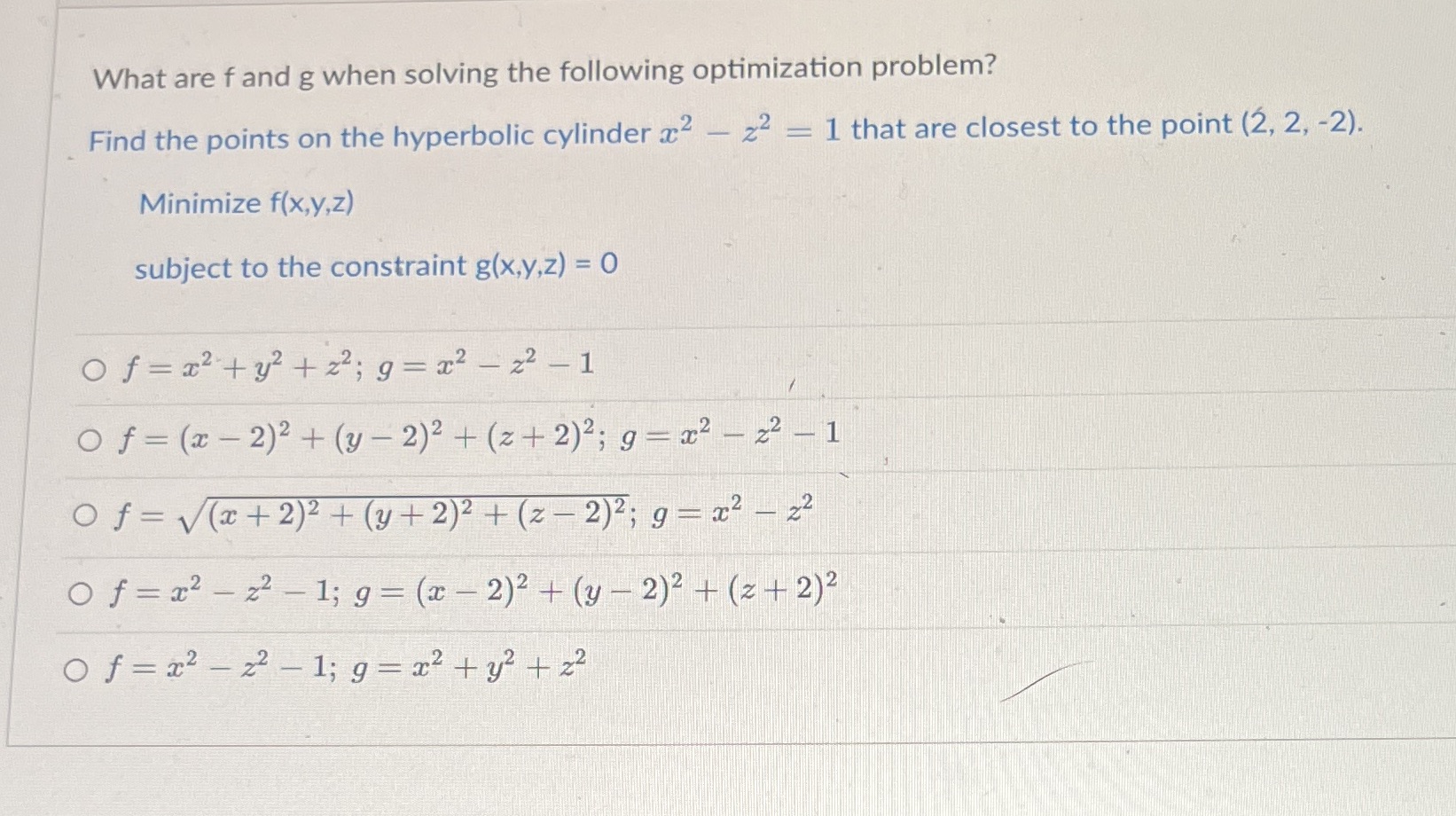
What are f and g when solving the following optimization problem? Find the points on the hyperbolic cylinder x2 - 22 = 1 that are closest to the point (2, 2, -2). Minimize f(x,y,z) subject to the constraint g(x,y,z) = 0 Of = x2 + y2 + 22; g = 12 - 22-1 Of = (x - 2)2 + (y - 2)2 + ( 2 + 2)2; 9- 202 - 22 - 1 Of = V(x + 2)2 + ( y + 2)2 + ( 2 - 2)2; 9- 22- 22 Of =2 - 22 - 1; g = (2 - 2)2 + (y - 2)2 + (2+ 2)2 of = x2 - 22 -1; 9=12+ 2+ z2