What I have to work with:

Any help would be greatly appreciated. This is for project management

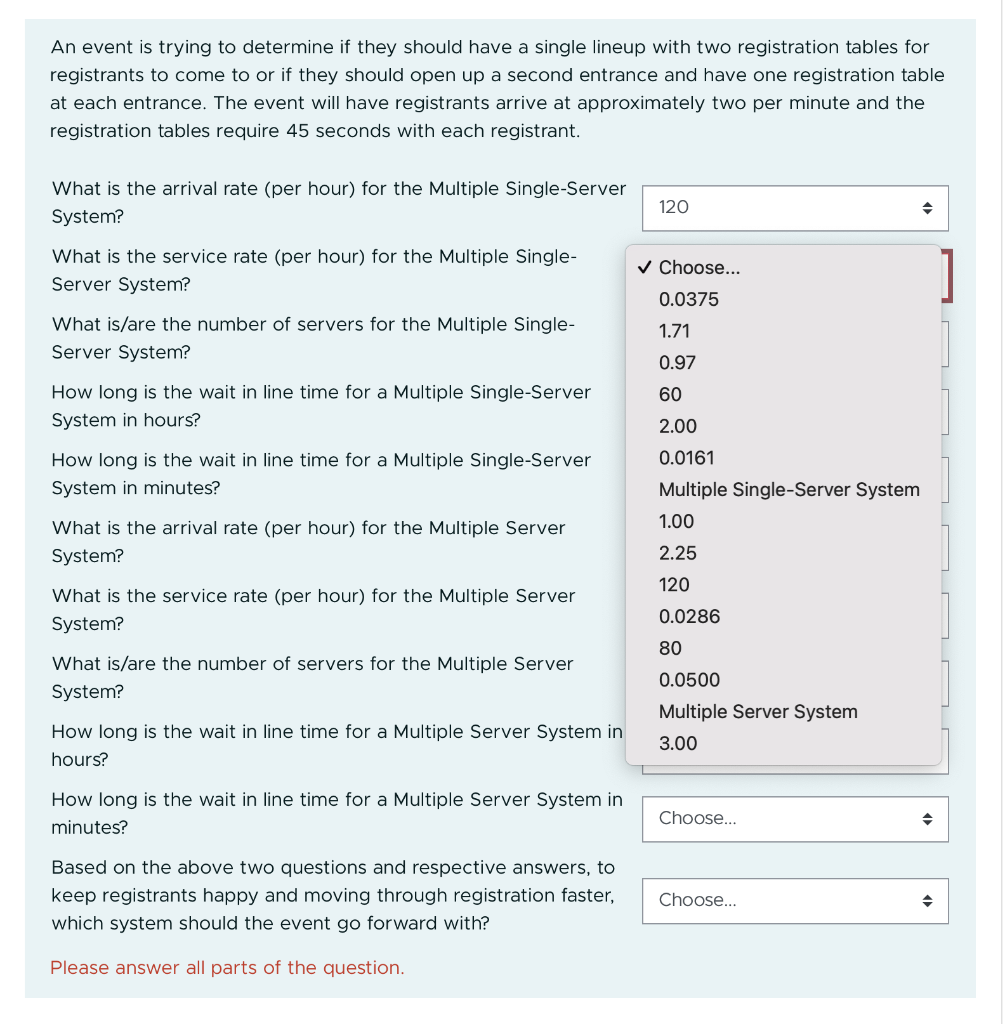
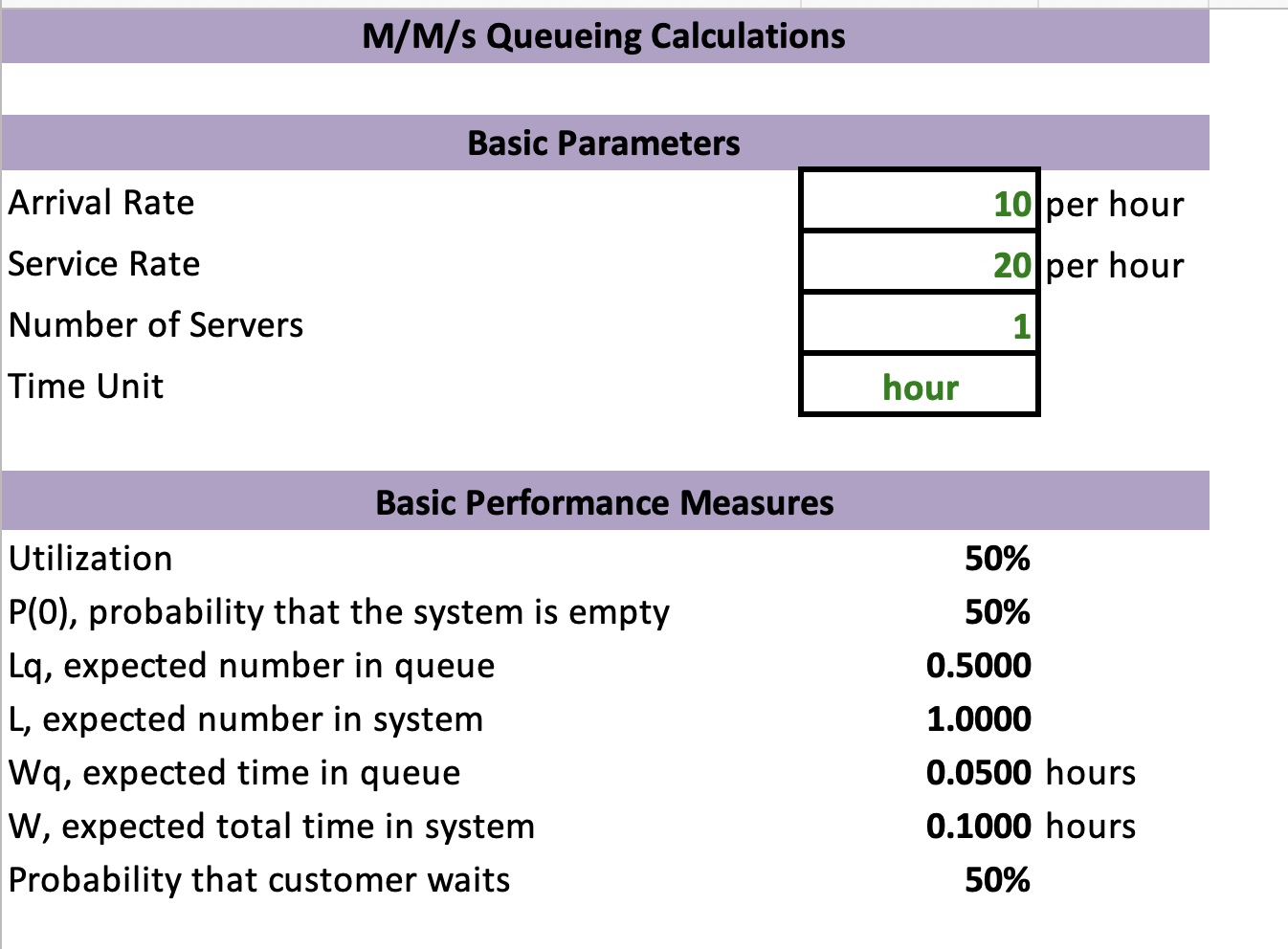
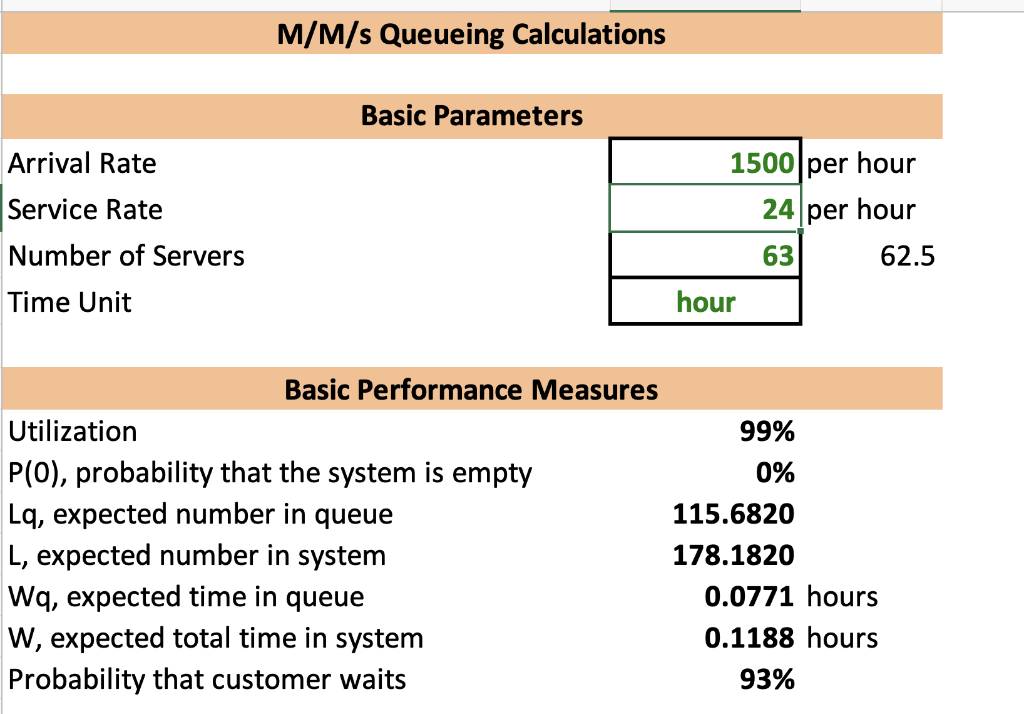
An event is trying to determine if they should have a single lineup with two registration tables for registrants to come to or if they should open up a second entrance and have one registration table at each entrance. The event will have registrants arrive at approximately two per minute and the registration tables require 45 seconds with each registrant. What is the arrival rate (per hour) for the Multiple Single-Server System? What is the service rate (per hour) for the Multiple SingleServer System? What is/are the number of servers for the Multiple SingleServer System? How long is the wait in line time for a Multiple Single-Server System in hours? How long is the wait in line time for a Multiple Single-Server System in minutes? What is the arrival rate (per hour) for the Multiple Server System? What is the service rate (per hour) for the Multiple Server System? What is/are the number of servers for the Multiple Server System? How long is the wait in line time for a Multiple Server System in hours? How long is the wait in line time for a Multiple Server System in minutes? Based on the above two questions and respective answers, to keep registrants happy and moving through registration faster, which system should the event go forward with? Please answer all parts of the question. M/M/s Queueing Calculations Basic Parameters Arrival Rate Service Rate Number of Servers Time Unit \begin{tabular}{|r|l} \hline 10 & per hour \\ per hour \\ \cline { 1 - 1 } & \\ \cline { 1 - 1 } hour \\ \hline \end{tabular} Basic Performance Measures Utilization P(0), probability that the system is empty Lq, expected number in queue L, expected number in system 50% 50% 0.5000 1.0000 Wq, expected time in queue 0.0500 hours W, expected total time in system 0.1000 hours Probability that customer waits 50% M/M/s Queueing Calculations Basic Parameters Arrival Rate Service Rate Number of Servers Time Unit \begin{tabular}{|r||r|} \hline 1500 & per hour \\ \hline 24 & per hour \\ \hline 63 & 62.5hour \\ \cline { 1 - 1 } & \end{tabular} Basic Performance Measures Utilization 99% P(0), probability that the system is empty 0% Lq, expected number in queue 115.6820 L, expected number in system 178.1820 Wq, expected time in queue 0.0771 hours W, expected total time in system 0.1188 hours Probability that customer waits 93%