What is a random variable?

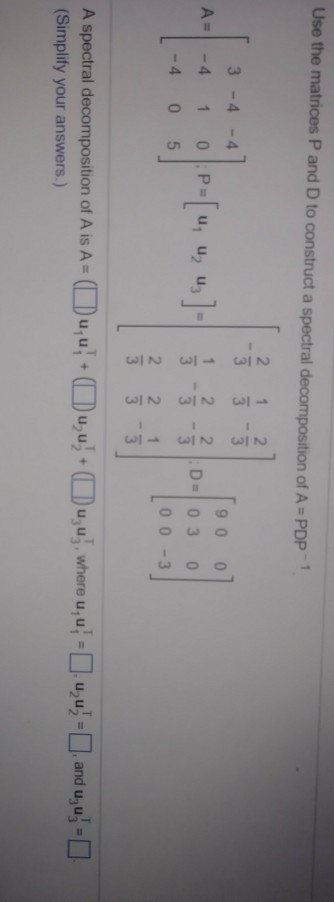
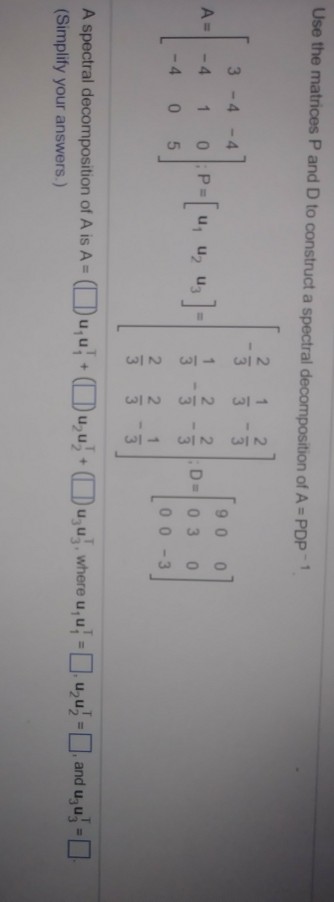
Problem 2. The eigenvalues of the following matrix are 5, 0, -1. Find the associated eigenvectors manually, and then use those to find an orthogonal diagonalization. 1 2 OO A = 2 4 0 0 1 You may use Matlab or a calculator to do any difficult computations, but do not use it to find the eigenvectors or orthogonal diagonalization directly. (b) Use you answer from part (a) to find the spectral decomposition of A. You may use Matlab to do the spectral decomposition computations, but not to find the spectral decom- position directly. Write your answer in the form described in Problem (1b), except now it will be in the form AlM1 + 2M2 + 13M3 for some M1, M2, and M3.Use the matrices P and D to construct a spectral decomposition of A = PDP - 1 9 0 O A= 0 : P = [ U , U2 Us] = NIm - Im NIM NIM NIM - IM - Im NIM NIM D=03 O 0 O A spectral decomposition of A is A = (Du, u, + (Du,u) + (Du,uj, where u, u! = . uzu) =, and ugu] =] (Simplify your answers.)4.1 Two Types of Random Variables 4.2. Probability Distributions for Discrete Random Variables 1. What is a random variable? 2. Give examples for discrete random variable, continuous random variableChi Squared and T Distribution[2 points} Let Vn ~ )1; 2 n and Tn ~ tn for all positive integers n. [a] Find numbers an and bn such that aan bn]I converges in distribution to NEIL 1]. [1 point} [b] Show that T 2 n Hn+T 2 n I has a Beta distribution. Specifyr the para meters of the Beta distribution. [1 point] Hirrt: You should be able to do part [b] by using the Beta Gamma connection. 4. Chi Squared and T Distributinn[2 points} Let V" N x: and Tn w in for all positive integers n. {3.} Find numbers an and {In such that an\"; Ian] converges in distribution to N[,1}. [1 point] [b} Show that T3,? [n+ TE} has a. Beta distribution. Specify the parameters of the Beta. distribution. {1 point] Hint: 1tron should be able to do part {b} h}...r using the Beta Gamma connection