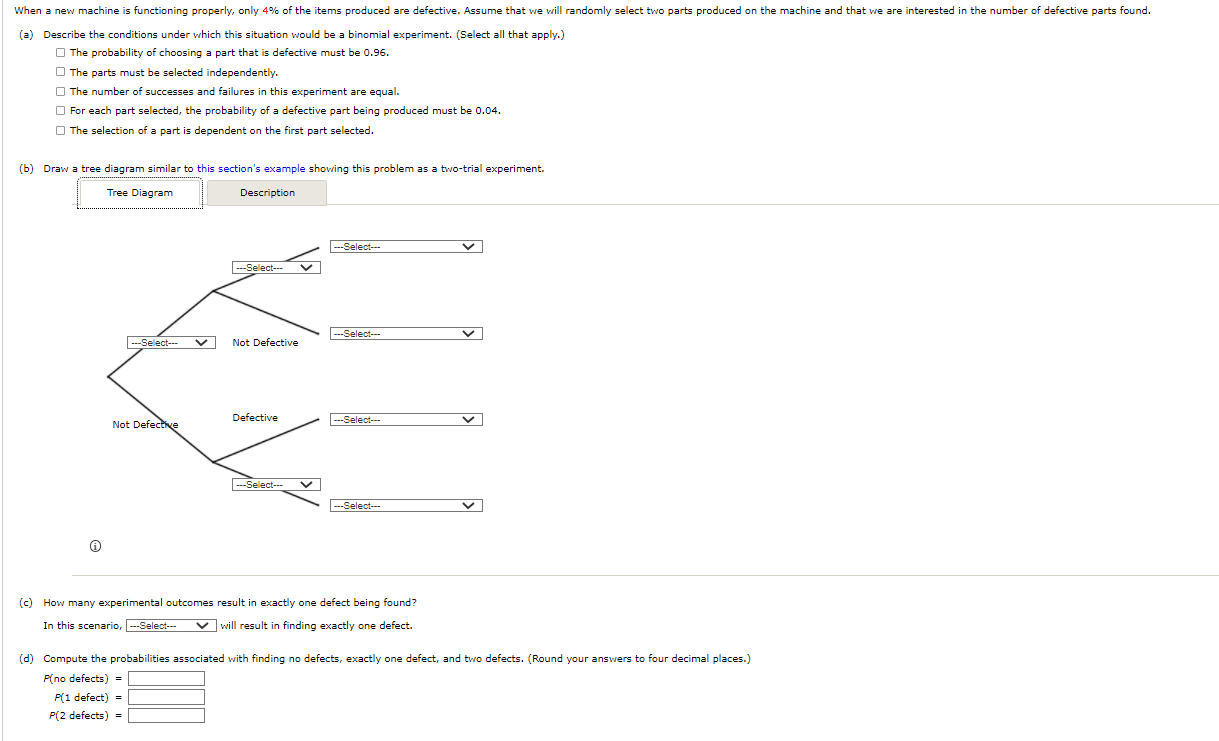
When a new machine is functioning properly, only 4% of the items produced are defective. Assume that we will randomly select two parts produced on the machine and that we are interested in the number of defective parts found. (a) Describe the conditions under which this situation would be a binomial experiment. (Select all that apply.) O The probability of choosing a part that is defective must be 0.96. O The parts must be selected independently. O The number of successes and failures in this experiment are equal. O For each part selected, the probability of a defective part being produced must be 0.04. O The selection of a part is dependent on the first part selected. (b) Draw a tree diagram similar to this section's example showing this problem as a two-trial experiment. Tree Diagram Description --Select-- ---Select--- ---Select-- v ---Select--- Not Defective Not Defective Defective ---Select--- ---Select--- ---Select--. v (c) How many experimental outcomes result in exactly one defect being found? In this scenario, [--Select- will result in finding exactly one defect. (d) Compute the probabilities associated with finding no defects, exactly one defect, and two defects. (Round your answers to four decimal places.) P(no defects) = P(1 defect) = P(2 defects) =