Question: When are two random samples independent? Random samples are independent by nature of random sampling. When sample data drawn from one population are related to

When are two random samples independent?

Random samples are independent by nature of random sampling.

When sample data drawn from one population are related to the selection of data from the other population.

When sample data drawn from one population are somewhat unrelated to the selection of data from the other population.

When sample data drawn from one population are completely unrelated to the selection of data from the other population.

When are two random samples dependent?

When each data value in one sample can be paired with a corresponding data value in the other sample.

When sample data drawn from one population are somewhat unrelated to the selection of data from the other population.

When sample data drawn from one population are completely unrelated to the selection of data from the other population.

Random samples are dependent by nature of random sampling.

Given that the standard deviations for two populations are unknown, choose the best answer.

Which of the following correctly calculates the standard error used to determine the margin of error for estimating the difference in means of two independent samples?

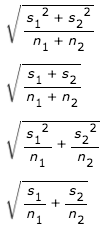
When are two random samples independent?Random samples are independent by nature of

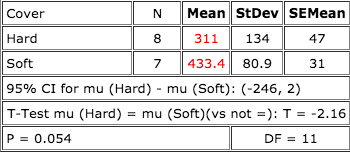
random sampling.When sample data drawn from one population are related to the

\fCover N Mean StDev SEMean Hard 8 311 134 47 Soft 7 433.4 80.9 31 95% CI for mu (Hard) - mu (Soft): (-246, 2) T-Test mu (Hard) = mu (Soft) (vs not =): T = -2.16 P = 0.054 DF = 11

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Part 1 of 4 - Random draw from Ch 20 Question 1 of 10 1.0 Points Each person in a random sample of 2000 likely voters (as defined by a professional polling organization) was questioned about his or...

In 1965, about 44% of the U.S. adult population had never smoked cigarettes. A national health survey of 1472 U.S. adults (presumably selected randomly) during 2010 revealed that 677 had never smoked...

Chapter 7 Inferential Statistics: Estimation and Hypothesis Androgen (ng/ml) at Adult Time of Injection Androgen (ng/ml) 30 Male 4.79 Minutes After Injection 18.53 7.39 13.74 7.91 7.30 0.52 10 4.85...

Given summary about this article the most important Humans inherit artificial intelligence biases Luca Vicente & Helena Matute * Artificial intelligence recommendations are sometimes erroneous and...

Questions: 1. Would you classify consecutive week or consecutive day sampling as bad sampling? If yes, what kind is it (i.e., convenience, biased, voluntary response, or all)? 2. If it is bad...

Hi there! I'm really struggling with this assignment wicked really appreciate some help with the answers for revision Assignment 01 ASSIGNMENT 01 Unique Nr.: 798531 Fixed closing date: 13 MAY 2021...

When are two random samples dependent? When each data value in one sample can be paired with a corresponding data value in the other sample. When sample data drawn from one population are completely...

For each quantity in boldface Questions 1-4 ask you to determine which is a parameter and which is a statistic. Question 1 24% of all the M&Ms produced are blue M&Ms - but in a small package of M&M's...

MBA 5652, Research Methods Course Syllabus Course Description Business research methods will guide students in advancing their knowledge of different research principles and their applicability in...

URGENT 38. Recall that a confidence interval is too small if the number being estimated is larger than every number in the confidence interval. Similarly, a confidence interval is too large if the...

Refer to the Market for Good X above. Po-$5, P1-$35, P2=$10, P=$15, Q1-20, Q2-80, and Q'-40. The government imposes a price floor of Px=$25. What is the Total Dead Weight Loss? (Do not include the...

Will an investor earn more if interest is compounded semiannually or if the investment only pays simple interest? Explain.

( Classification ) The following items are found in the financial statements. Discount on bonds payable. Interest expense ( credit balance ) . Unamortized bond issue costs. Gain on repurchase of...

32. alo The fixed assets have estimated useful lives as follows: Building - 31.5 years Computer Equipment - 5.0 years Office Equipment - 7.0 years Use the straight-line method of depreciation...