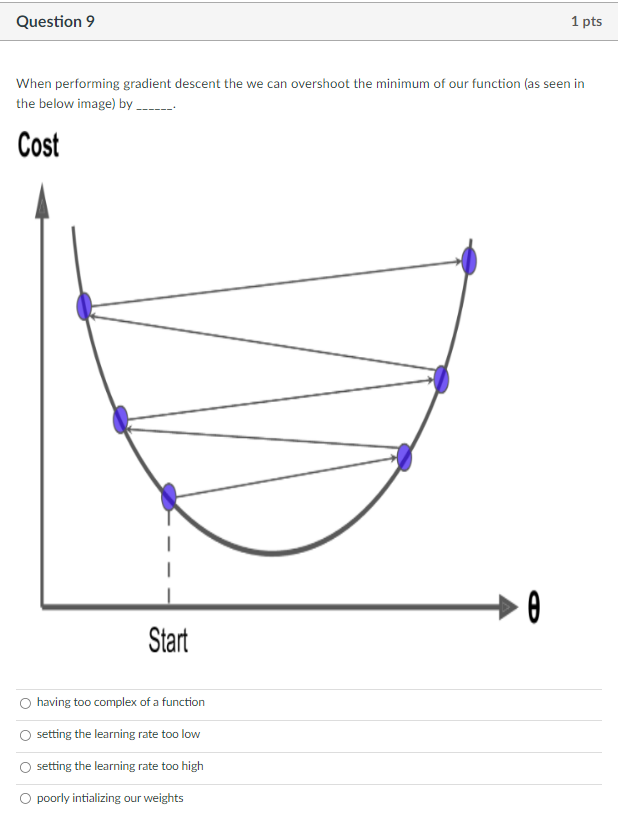
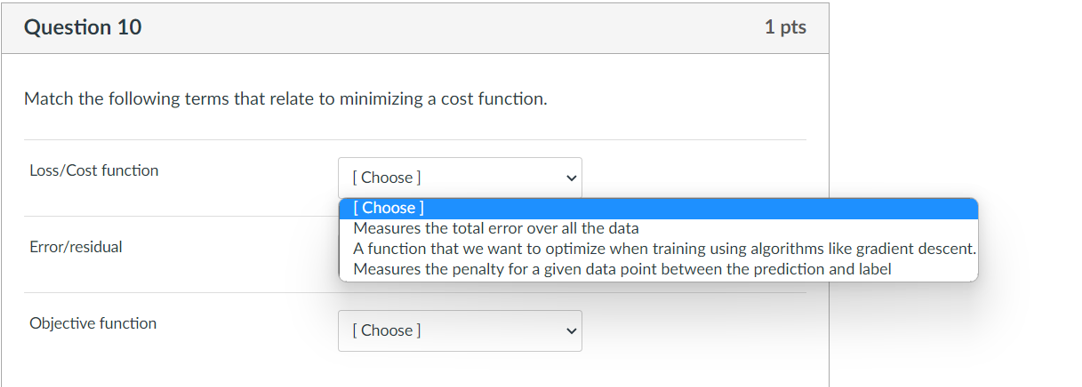
When minimizing the sum of squared errors J(w)=minwi=1m(f(xi;w)yi)2 for Least Mean Squares we want to update our weights using which of the following: the closed form equation the negative gradient the postive gradient the integral Online learning is when we update our model based on all data samples none of the above one data sample at a time a subset of data samples Batch learning is when we update our model based on none of the above one data sample at a time all data samples a subset of data samples When performing gradient descent the we can overshoot the minimum of our function (as seen in the below image) by Cost having too complex of a function setting the learning rate too low setting the learning rate too high poorly intializing our weights Match the following terms that relate to minimizing a cost function. Loss/Cost function Error/residual Objective function