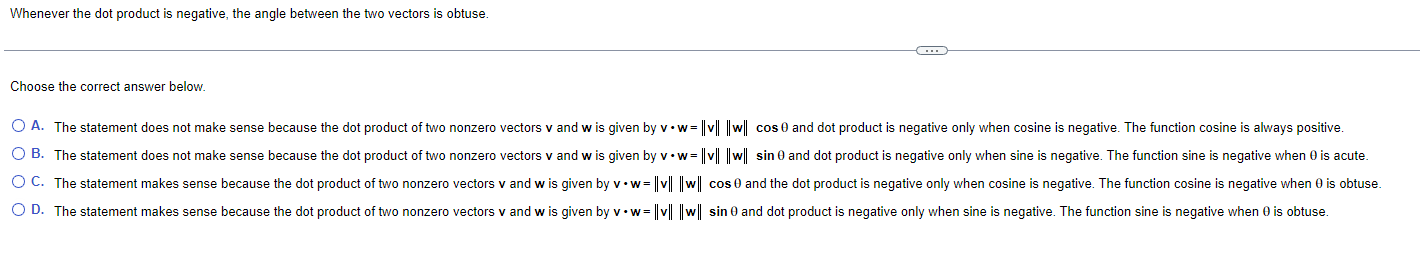
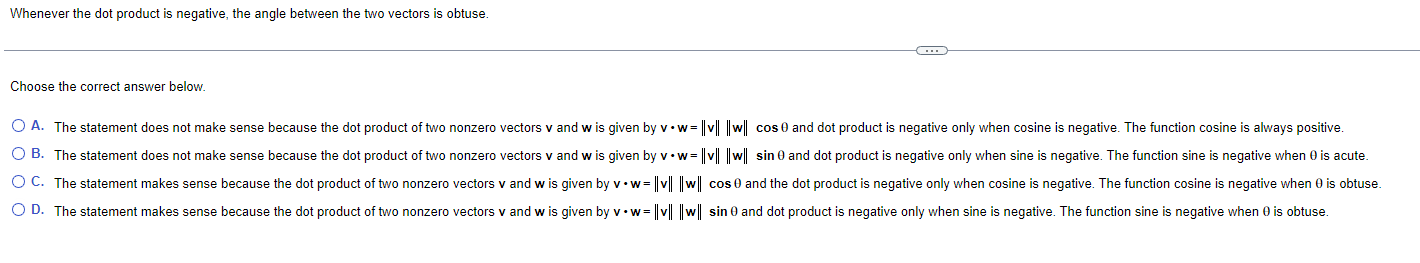
Whenever the dot product is negative. the angle between the two vectors is obtuse Choose the correct answer below. 0 A- The statement does not make sense because the dot product of two nonzero vectors v and w is given by v -w= \"tall \"in" cost} and dot product is negative only when cosine ls negative. The tundion cosine is always posillve OB. OC. The statement does not make sense because the dot product of two nonzero vectors \ and w is given by v -w= \"UH |lw|| sin 9 and dot product ls negative only when sine is negative The function sine is negative when 9 is acute The statemenl makes sense because the dot product oftwo nonzero veclors v and w is given by v -w= "v" "w" cos and the dot product is negallve only when cosine is negative The function cosine is negative when 9 is obtuse. O D- The statement makes sense because the dot. product oftwo nonzero vectors v and w is given by v -w= "v" "w" sin 9 and dot product is negative only when sine is negatlve. The functlon sine is negatlve when 9 is obtuse