Where did the DCF @ 17 % come from?

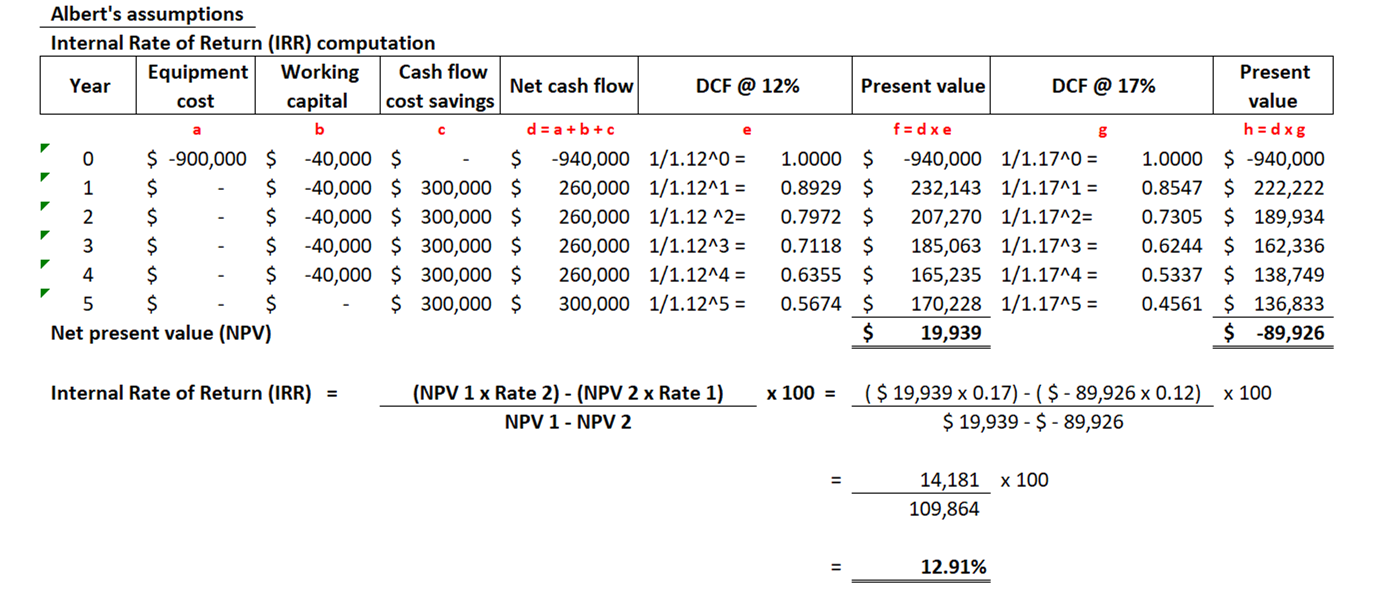
The estimated purchase price for the equipment required to move the operation in-house would be $900,000. Additional net working capital to support production (in the form of cash used in Inventory,

AR net of AP) would be needed in the amount of $40,000 per year starting in year 0 and through all years of the project to support production as raw materials will be required in year o and all years to

run the new equipment and produce components to replace those purchased from the vendor..

The current spending on this component (i.e. annual spend pool) is $1,500,000. The estimated cash flow savings of bringing the process in-house is 20% or annual savings of $300,000. This

includes the additional labor and overhead costs required.

Finally, the equipment required is anticipated to have a somewhat short useful life, as a new wave of technology is on the horizon. Therefore, it is anticipated that the equipment will be sold after the end of the project (the last year of generated cash flow) for $50,000. (i.e. the terminal value).

As part of your research, you have sought input from a number of stakeholders. Each has raised important

points to consider in your analysis and recommendation. Some of the points and assumptions are purely

financial. Others touch on additional concerns and opportunities.

1. Albert, your colleague from Accounting, recommends using the base assumptions above: 5-year project life, flat annual savings, and 12% discount rate. Albert does not feel the equipment will have

any terminal value due to advancements in technology.

Albert's assumptions Internal Rate of Return (IRR) computation Equipment Working Cash flow Present Year Net cash flow DCF @ 12% Present value DCF @ 17% cost capital cost savings value a b d= a +b+c f =dxe h =dxg $ -900,000 $ -40,000 -940,000 1/1.1240 = 1.0000 $ -940,000 1/1.17^0 = 1.0000 $ -940,000 NPO S -40,000 $ 300,000 260,000 1/1.12^1 = 0.8929 $ 232,143 1/1.17^1 = 0.8547 $ 222,222 $ -40,000 $ 300,000 $ 260,000 1/1.12 ^2= 0.7972 207,270 1/1.17^2= 0.7305 $ 189,934 $ -40,000 $ 300,000 $ 260,000 1/1.1243 = 0.7118 185,063 1/1.17^3 = 0.6244 $ 162,336 UI A WI -40,000 $ 300,000 $ 260,000 1/1.12^4 = 0.6355 $ 165,235 1/1.17^4 = 0.5337 138,749 $ 300,000 $ 300,000 1/1.1215 = 0.5674 $ 170,228 1/1.17^5 = 0.4561 $ 136,833 Net present value (NPV) 19,939 $ -89,926 Internal Rate of Return (IRR) = (NPV 1 x Rate 2) - (NPV 2 x Rate 1) x 100 = ( $ 19,939 x 0.17) - ( $ - 89,926 x 0.12) x 100 NPV 1 - NPV 2 $ 19,939 - $ - 89,926 = 14,181 x 100 109,864 = 12.91%