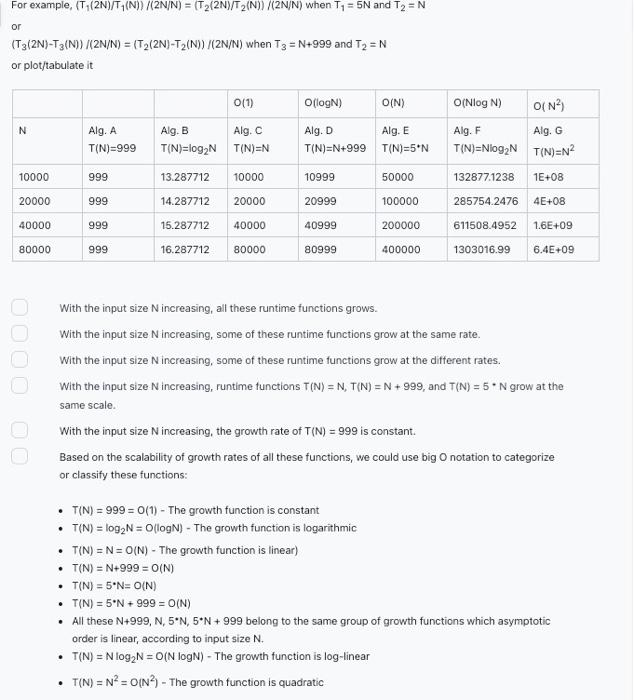
Which statements are correct about these following seven runtime functions? There are multiple correct answers! 1. T(N)=999 2. T(N)=log2N 3. T(N)=N 4. T(N)=N+999 5. T(N)=5N 6. T(N)=Nlog2N 7. T(N)=N2 Hints: 1) The order of a function describes how the function scales as the input(s) increases to infinite. Seven typical functions are in an increasing order: 2) If the growth rates of two functions are the same, these two functions belong to the same time complexity group, denoted as in the big O notation: For example, (T1(2N)/T1(N))/(2N/N)=(T2(2N)/T2(N))/(2N/N) when T1=5N and T2=N or (T3(2N)T3(N))/(2N/N)=(T2(2N)T2(N))/(2N/N) when T3=N+999 and T2=N or plot/tabulate it With the input size N increasing, all these runtime functions grows. With the input size N increasing, some of these runtime functions grow at the same rate. With the input size N increasing, some of these runtime functions grow at the different rates. With the input size N increasing, runtime functions T(N)=N,T(N)=N+999, and T(N)=5N grow at the same scale. With the input size N increasing, the growth rate of T(N)=999 is constant. Based on the scalability of growth rates of all these functions, we could use big O notation to categorize or classify these functions: - T(N)=999=O(1) - The growth function is constant - T(N)=log2N=O(logN) - The growth function is logarithmic - T(N)=N=O(N) - The growth function is linear) - T(N)=N+999=O(N) - T(N)=5N=O(N) - T(N)=5N+999=O(N) - All these N+999,N,5N,5N+999 belong to the same group of growth functions which asymptotic order is linear, according to input size N. - T(N)=Nlog2N=O(NlogN) - The growth function is log-linear - T(N)=N2=O(N2) - The growth function is quadratic