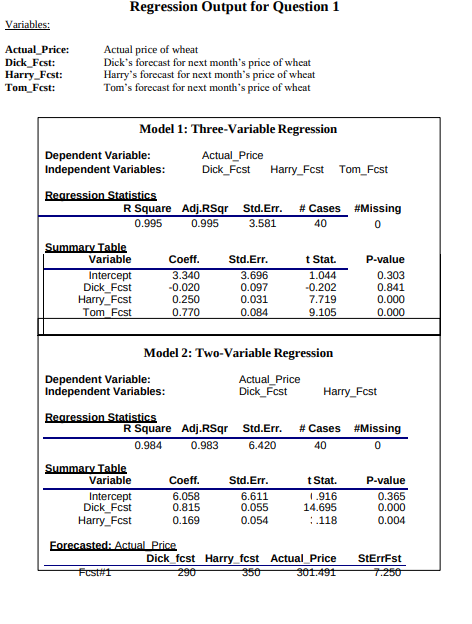
While working on the Breakfast Foods case, one team developed two models for predicting the actual price of wheat. FSBstats outputs for both models are provided on the next page. (a) Use the provided output (and coefficient estimates there) to write down the equation of the best fit line for the "Two-Variable" regression (Model 2). Furthermore, what is your best guess for the distribution of the error term? (2 points) (b) If we use the "Three-Variable" regression (Model 1) to forecast Actual_Price, can the standard error of the forecast be smaller than 3.5? Explain your answer. (3 points) (c) Use the "Two-Variable" regression (Model 2) to provide an estimate of the probability that Actual_Price will be below $310 when Dick's forecast is $290 and Harry's forecast is $350. (5 points).Regression Output for Question 1 Variables: Actual Price: Actual price of wheat Dick Fest: Harry_Fest: Dick's forecast for next month's price of wheat Harry's forecast for next month's price of wheat Tom_Fest: Tom's forecast for next month's price of wheat Model 1: Three-Variable Regression Dependent Variable: Actual_Price Independent Variables: Dick_Fest Harry_Fest Tom_Fest Regression Statistics R Square Adj.RSqr Std.Err. # Cases #Missing 0.995 0.995 3.581 40 Summary Table Variable Coeff. Std.Err. t Stat. P-value Intercept 3.340 3.696 1.044 0.303 Dick Fest -0.020 0.097 0.202 0.841 Harry_Fest 0.250 0.031 7.719 0.000 Tom Fest 0.770 0.084 9.105 0.000 Model 2: Two-Variable Regression Dependent Variable: Actual Price Independent Variables: Dick_Fest Harry_Fest Regression Statistics R Square Adj.RSqr Std.Err. # Cases #Missing 0.984 0.983 6.420 40 0 Summary Table Variable Coeff. Std.Err. t Stat P-value Intercept 6.058 6.611 1.916 0.365 Dick Fest 0.815 0.055 14.695 0.000 Harry_Fest 0.169 0.054 :.118 0.004 Forecasted: Actual Price Dick_fest Harry_fest Actual_Price StErrFst 290 50 UL.491Question 1 continued... (d) Use the "Two-Variable" regression (Model 2) to provide a 99.7% confidence interval for the change in Actual_Price when Harry_Fest increases by $1 and Dick_Fest remains unchanged. (5 points) (e) Use the "Two-Variable" regression (Model 2) to provide a 95% confidence interval for the change in Actual_Price when Dick_Fost decreases by $2 and Harry_Fest remains unchanged. (5 points)