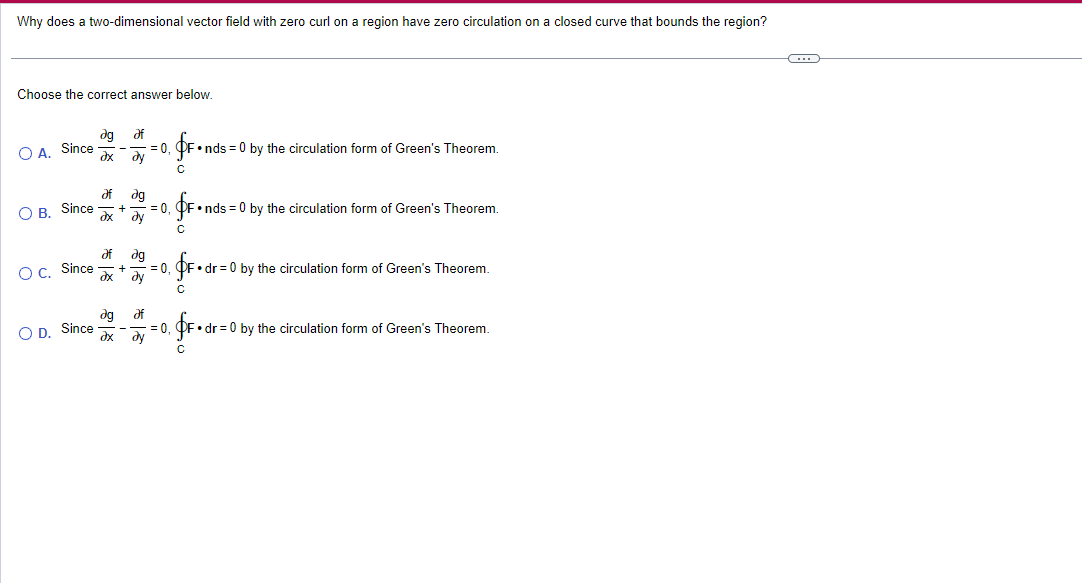
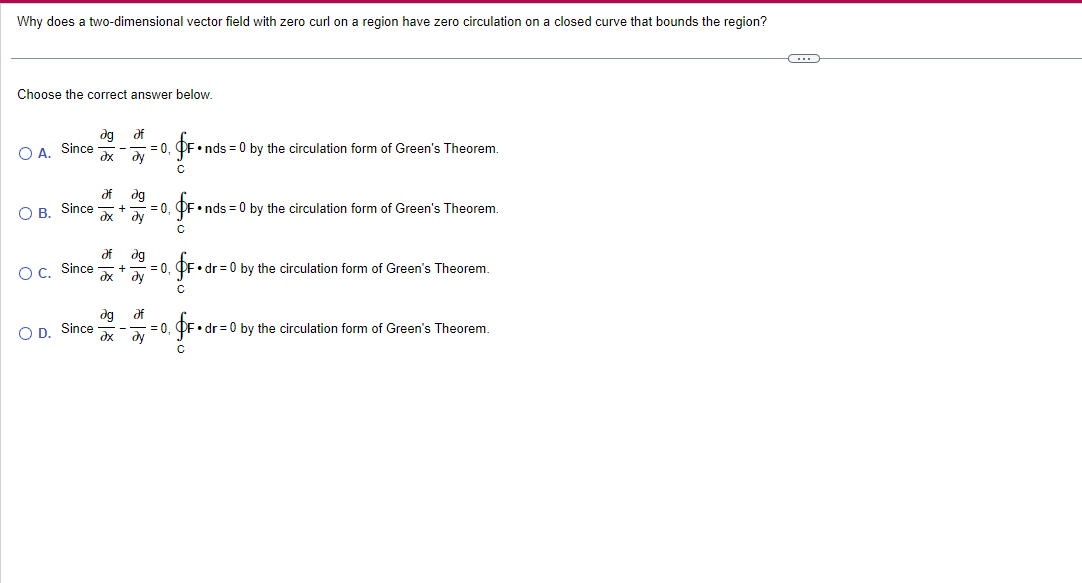
Question: Why does a twodimensional vector eld with zero curi on a region have zero circulation on a closed curve that bounds the region? Choose the

![I], 4} Inds = U by the circulation form of Green's Theorem.](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6664900f1d4c5_5116664900f06441.jpg)
Why does a twodimensional vector eld with zero curi on a region have zero circulation on a closed curve that bounds the region? Choose the correct answer below. at O A. Since 3 E = I], 4} Inds = U by the circulation form of Green's Theorem. 6 3f 39 O B. Since 3 + E = i], 4']: mos = U by the circulation form of Green's Theorem. 0 3f 439 O C. Since 3 + a = I], 4'} -dr= by the circulation form of Green's Theorem. c 89 at O D. Since 3 E = I], q} ldr=E| by the circulation form of Green's Theorem. C Why does a two-dimensional vector field with zero divergence on a region have zero outward flux across a closed curve that bounds the region? Choose the correct answer below. ag O A. Since ax ay =0, OF . dr = 0 by the flux form of Green's Theorem. C ag of O B. Since ax dy - = 0, OF . nds = 0 by the flux form of Green's Theorem. C of O c. Since =0, OF . dr =0 by the flux form of Green's Theorem. C of dg O D. Since + =0, OF . nds = 0 by the flux form of Green's Theorem. C
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


