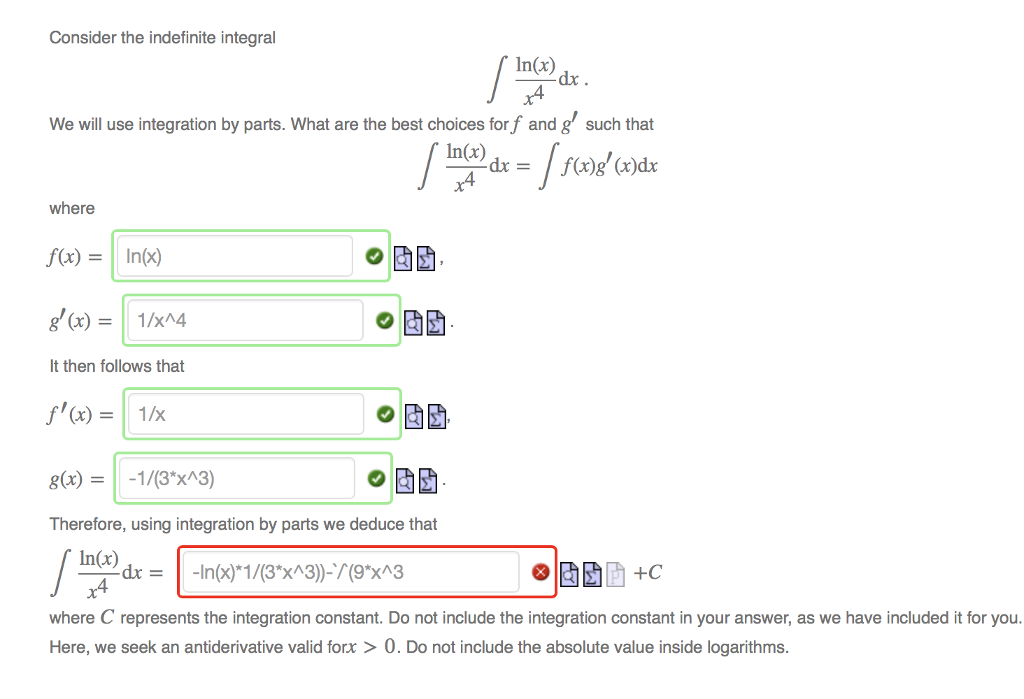
Question: Why is my integral incorrect? Please help. Consider the indefinite integral In(x) +4 We will use integration by parts. What are the best choices for
 Why is my integral incorrect? Please help.
Why is my integral incorrect? Please help.
Consider the indefinite integral In(x) +4 We will use integration by parts. What are the best choices for f and g' such that [In(x) dx = [ f(x)g'(x)dx where f(x) = In(x) g'(x) = 1/x^4 It then follows that f'(x) = 1/x g(x) = -1/(3*x^3) Therefore, using integration by parts we deduce that In(x) -In(x)*1/(3*x^3))-`/(9*x^3 -dx. -dx = BO+C where C represents the integration constant. Do not include the integration constant in your answer, as we have included it for you. Here, we seek an antiderivative valid forx > 0. Do not include the absolute value inside logarithms.
Step by Step Solution
There are 3 Steps involved in it
Solution We have to evaluate jene a dx fn gin d... View full answer

Get step-by-step solutions from verified subject matter experts


