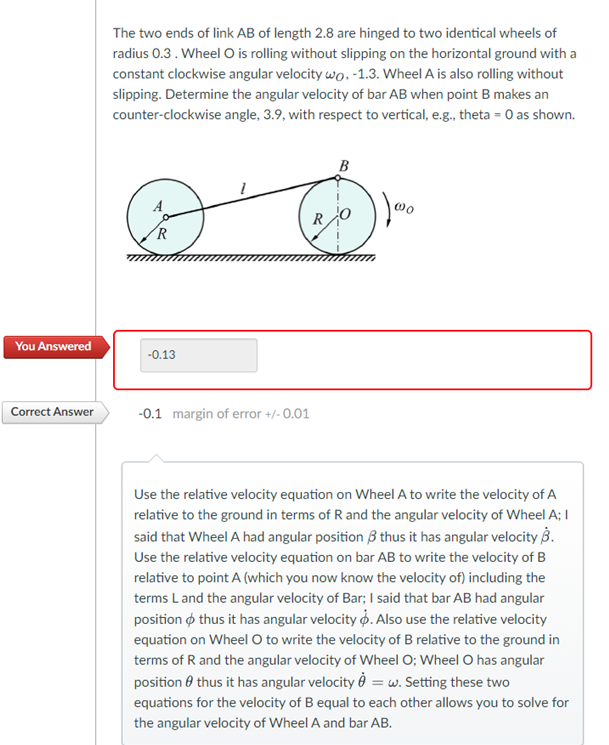
WILL GIVE THUMBS UP FOR CORRECT ANSWER The two ends of link $\backslash ($ A B $\backslash )$ of length $2\mathrm{.}8$ are hinged to two identical wheels of radius $0\mathrm{.}3.$ Wheel O is rolling without slipping on the horizontal ground with a constant clockwise angular velocity $\backslash (\backslash$omega$\_\{$O$\},-1\mathrm{.}3\backslash ).$ Wheel A is also rolling without slipping. Determine the angular velocity of bar $\backslash ($ A B $\backslash )$ when point $\backslash ($ B $\backslash )$ makes an counter$-$clockwise angle, $3\mathrm{.}9,$ with respect to vertical, e$.$g$.,$ theta $\backslash (=0\backslash )$ as shown.

Use the relative velocity equation on Wheel $\backslash ($ A $\backslash )$ to write the velocity of $\backslash ($ A $\backslash )$ relative to the ground in terms of $\backslash ($ R $\backslash )$ and the angular velocity of Wheel $\backslash ($ A ; I $\backslash )$ said that Wheel A had angular position $\backslash (\backslash$beta $\backslash )$ thus it has angular velocity $\backslash (\backslash$dot$\{\backslash$beta$\}\backslash ).$ Use the relative velocity equation on bar $\backslash ($ A B $\backslash )$ to write the velocity of $\backslash ($ B $\backslash )$ relative to point A $($which you now know the velocity of$)$ including the terms $\backslash ($ L $\backslash )$ and the angular velocity of Bar; I said that bar $\backslash ($ A B $\backslash )$ had angular position $\backslash (\backslash$phi $\backslash )$ thus it has angular velocity $\backslash (\backslash$dot$\{\backslash$phi$\}\backslash ).$ Also use the relative velocity equation on Wheel O to write the velocity of B relative to the ground in terms of $\backslash ($ R $\backslash )$ and the angular velocity of Wheel $\backslash ($ O $\backslash )$; Wheel $\backslash ($ O $\backslash )$ has angular position $\backslash (\backslash$theta $\backslash )$ thus it has angular velocity $\backslash (\backslash$dot$\{\backslash$theta$\}=\backslash$omega $\backslash ).$ Setting these two equations for the velocity of $\backslash ($ B $\backslash )$ equal to each other allows you to solve for the angular velocity of Wheel $\backslash ($ A $\backslash )$ and bar $\backslash ($ A B $\backslash ).$