WILL NOT BE SOLVED WITH EXCEL , MODEL AND IT'S CONSTRAINTS

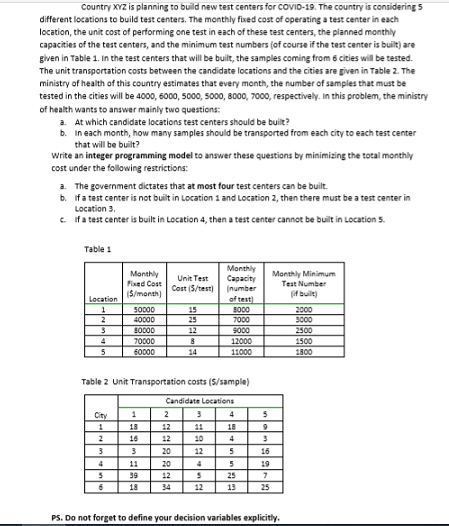
Country XYZ is planning to build new test centers for COVID-19. The country is considerings different locations to build test centers. The monthly fried cost of operating a test center in each location, the unit cost of performing one test in each of these test centers, the planned monthly capacities of the test centers, and the minimum test numbers of course if the test center is built are given in Table 1. In the test centers that will be built the samples coming from 6 cities will be tested The unit transportation costs between the candidate locations and the cities are given in Table 2. The ministry of health of this country estimates that every month, the number of samples that must be tested in the cities will be 4000, 5000, 5000, 5000, 8000, 7000, respectively. In this problem, the ministry of health wants to answer mainly two questions: a. At which candidate locations test centers should be built? b. in each month, how many samples should be transported from each city to each test center that will be built? write an integer programming model to answer these questions by minimizing the total monthly cost under the following restrictions: a. The government dictates that at most four test centers can be built b. fatest center is not built in Location 1 and Location 2, then there must be a test center in Location 3 c. If a test center is built in Location 4, then a test center cannot be built in Locations Table 1 Monthly Minimum Test Number built) Monthly Monthly Unit Test Capacity Fixed Cost Cost (S/test number $/month) oftest 50000 15 0 00 40000257000 30000 12 9000 70000 3 1 2000 60000 3000 2500 1500 1300 11000 Table 2 Unit Transportation costs (5/sample) Candidate Locations PS. Do not forget to define your decision variables explicitly. Country XYZ is planning to build new test centers for COVID-19. The country is considerings different locations to build test centers. The monthly fried cost of operating a test center in each location, the unit cost of performing one test in each of these test centers, the planned monthly capacities of the test centers, and the minimum test numbers of course if the test center is built are given in Table 1. In the test centers that will be built the samples coming from 6 cities will be tested The unit transportation costs between the candidate locations and the cities are given in Table 2. The ministry of health of this country estimates that every month, the number of samples that must be tested in the cities will be 4000, 5000, 5000, 5000, 8000, 7000, respectively. In this problem, the ministry of health wants to answer mainly two questions: a. At which candidate locations test centers should be built? b. in each month, how many samples should be transported from each city to each test center that will be built? write an integer programming model to answer these questions by minimizing the total monthly cost under the following restrictions: a. The government dictates that at most four test centers can be built b. fatest center is not built in Location 1 and Location 2, then there must be a test center in Location 3 c. If a test center is built in Location 4, then a test center cannot be built in Locations Table 1 Monthly Minimum Test Number built) Monthly Monthly Unit Test Capacity Fixed Cost Cost (S/test number $/month) oftest 50000 15 0 00 40000257000 30000 12 9000 70000 3 1 2000 60000 3000 2500 1500 1300 11000 Table 2 Unit Transportation costs (5/sample) Candidate Locations PS. Do not forget to define your decision variables explicitly