Question: With justification means that for example if the relation satisfies (i), then you need to prove it. If the relation doesn't satisfy (i), you need

With justification means that for example if the relation satisfies (i), then you need to prove it.

If the relation doesn't satisfy (i), you need to give one counterexample.

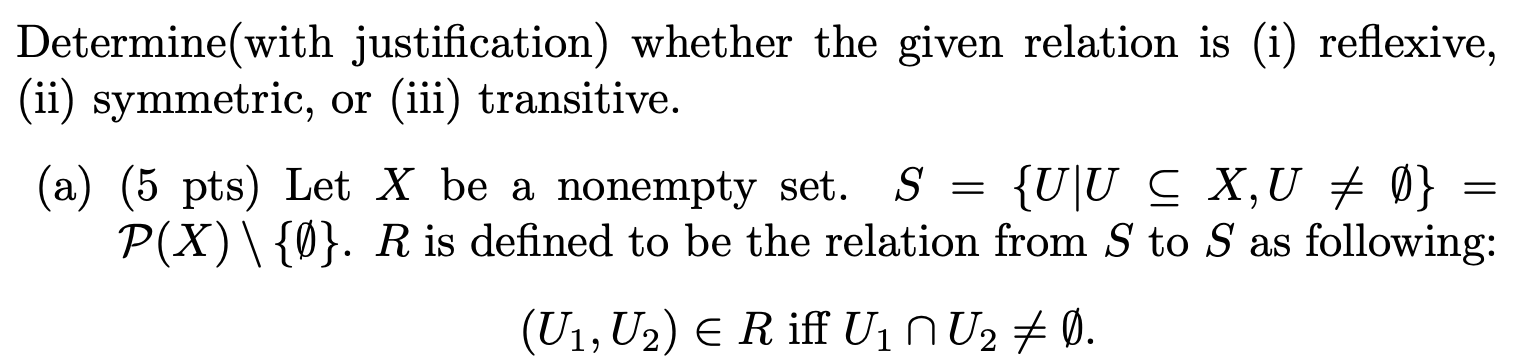
Determine(with justification) whether the given relation is (i) reflexive, (ii) symmetric, or (iii) transitive. (a) (5 pts) Let X be a nonempty set. S = {UU C X,U + 0} = P(X) \\ {}. R is defined to be the relation from S to S as following: (U1, U2) E Riff UInU2 + 0

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Mathematics and Politics HW # 1, Due 2/15/2017 Do any 8 out of the following 10 problems! 1. Consider the profile A A B A A A B B B B B B B B B A B B Who wins under: (a) The simple majority method...

MUST BE CORRECT ANSWERS A small software company has the following simplified cashflow, funded by shareholders' equity of 20,000 and a bank overdraft of 5000: Invoiced money received 2 months after...

Query Optimization and Equivalence Rules (20 points) Using the relational algebra to specify queries can be tedious at times, but it also has a big benefit that there are many different ways to state...

1. A player throws a fair die and simultaneously flips a fair coin. If the coin lands heads, then she wins twice, and if tails, then one-half of the value that appears on the die. Determine her...

3 ,,uoh "gram 3 Eww 3 m T mm H a 3 .2 ' m w .,.m.av>v 3. m. @3on we geonwoaoa mm H "with M'nr H E. wads + we A at. ES 0 3.8V WEE 3563 mo wow 23 E m \"9H .3 avgmeMm\" mnemagouom Aggy\"...

MATH 2600H 2017 Winter Assignment 3 Due March 21, 2017 1. Section 7.2 #25. Let S be the set of all strings in a's and b's, and de...ne C : S ! S by C (s) = as; for all s 2 S: (a) Is C one-to-one?...

answer the question clearly (a) What is the von Neumann bottleneck and why can it limit performance on today's RISC machines? [4 marks] (b) What computer architecture techniques are used to mitigate...

Write an alternative definition that is tail-recursive (iterative) and makes use of accumulator variables. [10 marks] Explain why your alternative definition executes more efficiently. [3 marks] 1...

Describe how to construct the function cpo ((D E), v) of two cpos (D, vD) and (E, vE). Prove that ((D E), v) is a cpo. (You may use facts about least upper bounds provided you state them clearly.)...

Selected comparative financial statements of Park Company follow. Required 1. Compute trend percents for all components of both statements using 2004 as the base year. (Round percents to one...

Give the formula for simple interest where I is the interest in dollars, P is the principal in dollars, r is the interest rate as a decimal, and t is the time period in years. por-t 100 IM A simple...

Megamind requires a new mind for $ 1 million Megamind determines that at the date of acquisition that will cost $ 1 4 0 , 0 0 0 to restore the land when the mining process is complete in five years...

Exam 29 The following credit sales are budgeted by Gonzalez Company. The company past experience indicates that 80% of the accounts receivable are collected in the month of sale, 20 percent in the...