With python programming:

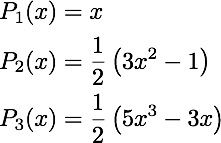
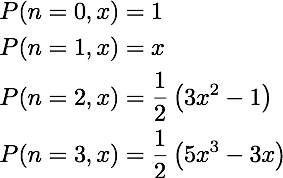
extend your legendre(n,x) function to support even higher order polynomials based on the Bonnet's recursion formula:

Now the argument n can be any non-negtive integers, and the function should still return the nth order Legendre polynomial of x.

--------------------------------------------------------------------------------------------------------------------------

def legendre(n, x): ### IMPLEMENT YOUR CODE BELOW ### return 0.

2 3 3 x 1212 2 P(n = 0, z) = 1 P(n = 1, z) = z 3x21 P(n = 3, z) =-(5c3-32) n+1