with steps plese

thd id that you will use is : 220110839

solve the last one Q 6 the iD:220110839 so

a1=2 ,a2=0 a3 =1 ,a4=1 ,a5=0 ,a6=8 ,a7=3 a8=9

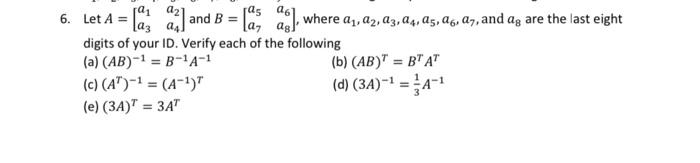
Let A=[a1a3a2a4] and B=[a5a7a6a8], where a1,a2,a3,a4,a5,a6,a7, and a8 are the last eight digits of your ID. Verify each of the following (a) (AB)1=B1A1 (b) (AB)T=BTAT (c) (AT)1=(A1)T (d) (3A)1=31A1 (e) (3A)T=3AT 1. Use parametric equations to describe the solution set of the linear equation a1x1+a2x2+ a3x3+a4x4=1, where the coefficients are the last 4 nonzero digits of your ID. (Example: if your ID is 214110008 , then the coefficients are: a1=4,a2=1,a3=1, and a4= 8.) 2. Find all values of k for which the augmented matrix [a1a3ka4a2a5] corresponds to a consistent linear system, where a1,a2,a3,a4, and a5 are the last five digits of your ID. (Example: if your ID is 214110008 , then the coefficients are: a1=1,a2=0,a3=0,a4= 0 and a5=8.) 3. Change the matrix a1a4a7a2a5a8a3a6a9100 to the reduced row echelon form, where a1,a2,a3,a4,a5,a6,a7,a8, and a9 are the nine digits of your ID from left to right. (Example: if your ID is 214110008, then the coefficients are: a1=2,a2=1,a3=4,a4= 1,a5=1,a6=0,a7=0,a8=0, and a9=8.) 4. Use Gaussian elimination method to solve the system {a1x1+a2x2+a3x3+a4x4=0a5x1+a6x2+a7x3+a8x4=0, where a1,a2,a3,a4,a5,a6,a7, and a8 are the last eight digits of your 1D. (Example: if your ID is 214110008 , then the coefficients are: a1=1,a2=4,a3=1,a4= 1,a5=0,a6=0,a7=0, and a8=8.) 5. Find all values of k, if any, that satisfy the equation k11Ta1a4a7a2a5a8a3a6a9k11=0, where a1,a2,a3,a4,a5,a6,a7,a8, and a9 are the nine digits of your ID from left to right. 6. Let A=[a1a3a2a4] and B=[a5a7a6a8], where a1,a2,a3,a4,a5,a6,a7, and a8 are the last eight digits of your ID. Verify each of the following (a) (AB)1=B1A1 (b) (AB)T=BTAT (c) (AT)1=(A1)T (d) (3A)1=31A1 (e) (3A)T=3AT