With the below information how do I answer e and f

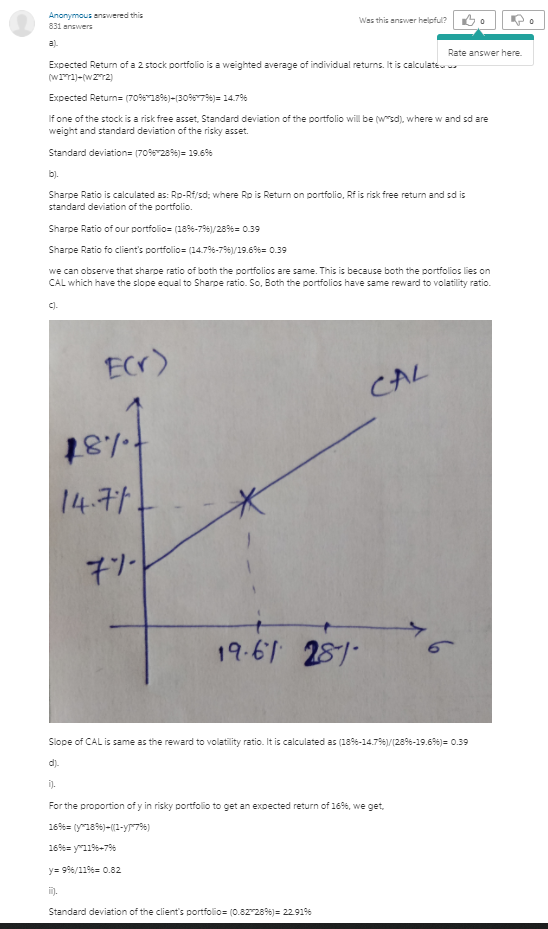
Problem 5 (40 marks). Assume that you manage a risky portfolio with an expected rate of return of 18% and a standard deviation of 28%. The T-bill rate (risk-free rate) is 7%. Your client chooses to invest 70% in the risky portfolio in your fund and 30% in a T-bill money market fund. We assume that investors use mean-variance utility: U = E(r) - 0.5 x Ao?, where E(r) is the expected return, A is the risk aversion coefficient and o is the variance of returns. a) What is the expected value and standard deviation of the rate of return on your client's portfolio? [4 marks] b) What is the reward-to-volatility ratio (Sharpe ratio) of your risky portfolio? What is the reward-to-volatility ratio (Sharpe ratio) of your client's risky portfolio? Comment on the relationship between these two Sharpe ratio calculated and explain the intuition behind. [8 marks] c) Draw the Capital Allocation Line (CAL) of your portfolio on an expected return- standard deviation diagram. What is the slope of the CAL? Show the position of your client on your fund's CAL. [6 marks] d) Suppose that your client decides to invest in your portfolio a proportion y of the total investment budget so that the overall portfolio will have an expected rate of return of 16% (i) What is the proportion y? [2 marks] (ii) What is the standard deviation of the rate of return on your client's portfolio? [3 marks] e) Your client's degree of risk aversion is A = 3.5. 2 FINA202 - Assignment 1 Cheng Zhang (i) What proportion, y, of the total investment should be invested in your risky fund? [2 marks] (ii) What is the expected value and standard deviation of the rate of return on your client's optimized portfolio? [4 marks] f) If your client's degree of risk aversion increases from A = 3.5 to A = 4.5. (i) What proportion, y, of the total investment should be invested in your risky fund? [2 marks] (ii) Comparing your answers to d)(i) and e)(i), what do you conclude about the relationship between the proportion y invested in the your fund and your client's attitude toward risk? [3 marks) (iii) Given that the optimal proportion of the risky asset in the complete portfolio is given by the equation y* = B(A)", where ry is the risk-free rate, E(Tp) is the expected return of the risky portfolio, ois variance of returns, and A is the risk aversion coefficient. For each of the variables on the right side of the equation, dis- cuss the impact of the variable's effect on y* and why the nature of the relationship makes sense intuitively. Assume the investor is risk averse. [6 marks] Was this answer helofu? 0 0 Anonymous answered this 831 answers a Rate answer here. Expected Return of a 2 stock portfolio is a weighted average of individual returns. It is calculate (WIT2)-(W2072) Expected Return= (7091896)-(3097%)= 14.796 If one of the stock is a risk free asset, Standard deviation of the portfolio will be wsd), where w and sd are weight and standard deviation of the risky asset. Standard deviation= 70%-289)= 19.6% b). Sharpe Ratio is calculated as: Ro-Rf/sd: where Rois Return on portfolio, Rfis risk free return and sd is standard deviation of the portfolio. Sharpe Ratio of our portfolio= (1896-796/2896= 0.39 Sharpe Ratio fo client's portfolio= (14.796-79/19.696= 0.39 we can observe that sharpe ratio of both the portfolios are same. This is because both the portfolios lies on CAL which have the slope equal to Sharpe ratio. So, Both the portfolios have same reward to volatility ratio. Ecr) CAL } 1871 14.711 77 19.61 281 Slope of CAL is same as the reward to volatility ratio. It is calculated as (1896-14.7%)/(2896-19.656)= 0.39 d) 0 For the proportion of y in risky portfolio to get an expected return of 16%, we get 16%= (y289)-11-y|7) 169= y1196+796 y = 99/11 0.82 i). Standard deviation of the client's portfolios (0.82 289) = 22.9196