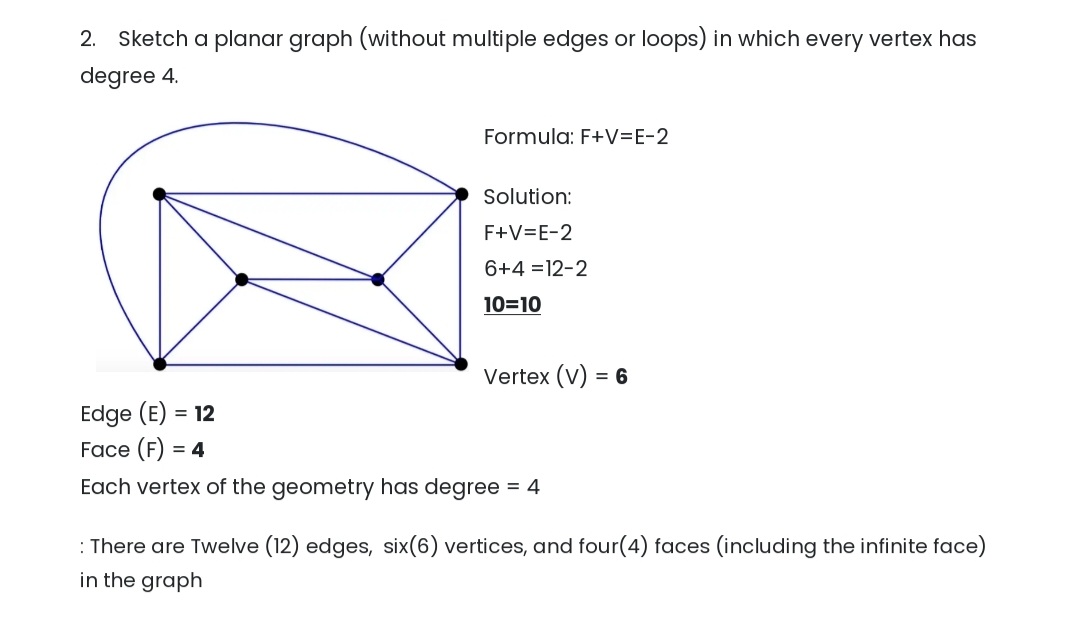
Question: with typewritten solution example below follow format 2. Sketch a planar graph (without multiple edges or loops) in which every vertex has degree 4. Formula:
with typewritten solution example below follow format

Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


