Question: Without solving explicitly, classify the critical points of the given first-order autonomous differential equation as either asymptotically stable or unstable. All constants are assumed

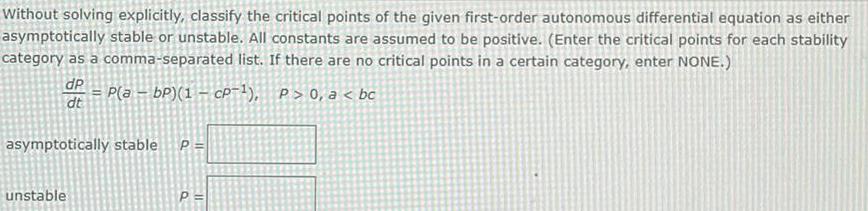
Without solving explicitly, classify the critical points of the given first-order autonomous differential equation as either asymptotically stable or unstable. All constants are assumed to be positive. (Enter the critical points for each stability category as a comma-separated list. If there are no critical points in a certain category, enter NONE.) dP dt = P(a bP)(1 CP-1), P> 0, a < bc asymptotically stable P= unstable P=

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Which expression is equivalent to tan(x) + cot(x)? COS 2 sec 2 cos(x) sin(x) sin(x) cos(x) 2 tan(x)

Applied Mathematics and Computation 95 (1998) 181192 Love dynamics: The case of linear couples Sergio Rinaldi 1 Centro Teoria dei Sistemi, CNR, Politecnico di Milano, Via Ponzio 34/5, 20133 Milan,...

2.7. Explicit Solutions to Dierential Equations 109 power (kw) 20 15 10 5 0 08:00 10:00 12:00 14:00 16:00 time 18:00 2.7 Explicit Solutions to Dierential Equations In the very rare case in which an...

seventh pages Chapter 3 Curve Sketching How much metal would be required to make a 400-mL soup can? What is the least amount of cardboard needed to build a box that holds 3000 cm3 of cereal? The...

Consider the following differential equation y^' =y(1+y)^2 (2-y)^3 find the critical points and Skitch the phase portrait of the given autonomous first-order differential equation. Classify each...

Consider the autonomous first - order differential equation y = y 2 y 3 Find the DISTINCT critical points and classify each as ( 1 ) AS for Asymptotically Stable, ( 2 ) US for Unstable or ( 3 ) SS...

Sec 2.1: Problem 4 Previous Problem Problem List Next Problem (1 point) Consider the autonomous first-order differential equation y' = (yev -gy)/e" Find the DISTINCT critical points and classify each...

Find the critical points and phase portrait of the given autonomous first-order differential equation. Classify each critical point as asymptotically stable, unstable, or semi-stable. By hand, sketch...

The most critical submission of the theory of computation has been to establish that the halting problem is not decidable. Give a clear statement of this result (you are not asked to prove it). [5...

I have literally posted the complete assignment information, can I please have some help with these two problems? MAT 375 Module Two Guided Activity: (Continuous) Dynamical Systems Our textbook has a...

A school has 4820 students. Five years later, the same school has 3850 students. If there was linear growth, the slope of this line would (numerically) be -194 (negative 194). Which of these shows...

Discuss how business analytics can be used in your workplace or profession to impact decision-making. Include the skills you possess to promote work in the discipline and those you need to acquire or...

When a syndicate of investment bank brokers and IPO, the firm that manages the is known as a underwriter B lead underwriter see derivative interest for participating organization

The force constant of a massless spring is 2 5 . 0 N / m . A mass of 0 . 4 5 kg is oscillating in simple harmonic motion at the end of the spring

Justice OConnor and the majority of the Court seem to believe that there must be some specific, identifiable individuals who have been discriminated against before race-conscious measures can be...

In court, Vinsons allegations were countered by Taylors version of the facts. Will there always be a your word against mine problem in sexual harassment cases? What could Vinson have done to...

What steps do you think Vinson should have taken when Taylor first pressed her for sex? Should she be blamed for having given in to him? Assuming that there was sexual harassment despite her...