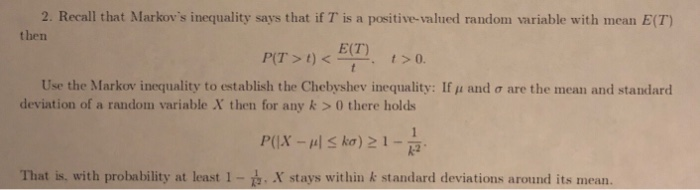
Workings needed

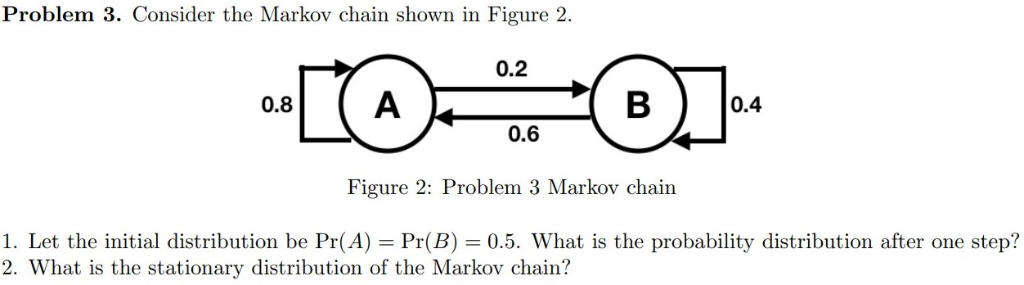
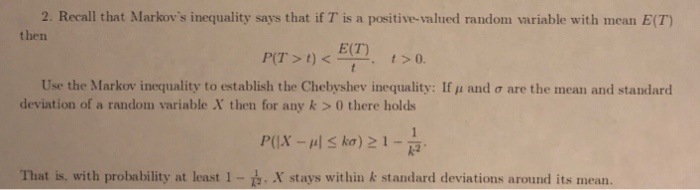
Consider a Markov chain {Xn : n = 0, 1, 2, ...} with state space {1, 2, 3} and one-step transition probability matrix O NIH NIH P = O 0 O (a) Mark O or X: ( ) The Markov chain is irreducible. ( ) The Markov chain is aperiodic. ( ) The Markov chain is transient. ( ) The Markov chain is recurrent. ( ) The Markov chain is null recurrent. ( ) The Markov chain is ergodic. (b) Calculate P(X5 = 1/X2 = 1). (c) Find limn + P(Xn = 1/X2 = 1).Problem 3. Consider the Markov chain shown in Figure 2. Figure 2: Problem 3 Markov chain 1. Let the initial distribution be Pr(A) : Pr(B) = 0.5. What is the probability distribution after one step? 2. What is the stationary distribution of the Markov chain? What are the main differences between traditional economics and behavioral economics? (in Traditional economics is mainly theoretical. Cl Behavioral economics does not take as a given that decision makers are rational. O Traditional economics assumes that decision makers are fully' informed. 2. Recall that Markov's inequality says that if T' is a positive-valued random variable with mean E(T) then E(T) P(T > 1 ) 0 there holds P(1X - #| Ska) 21 - 1 That is. with probability at least 1 - 2. X stays within & standard deviations around its mean