Would anyone be willing to help with this python code and include comments? Thanks!

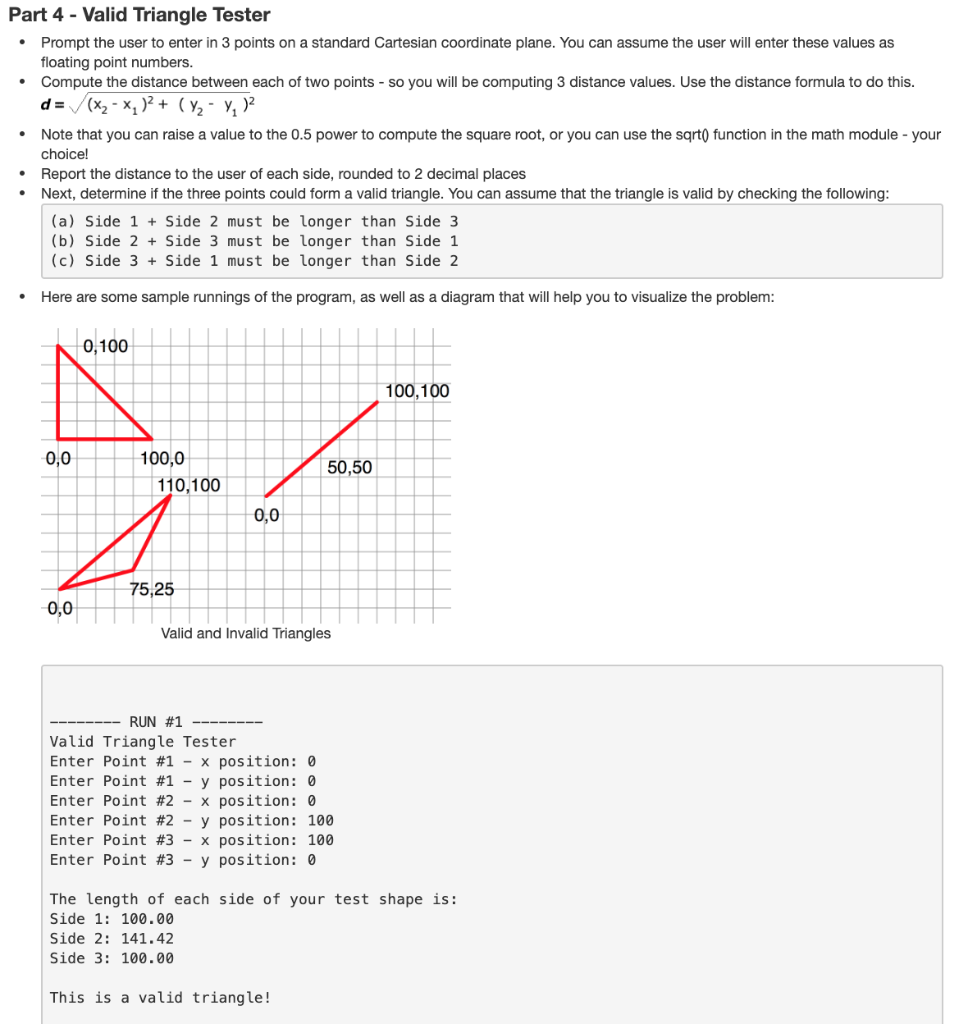
Part 4 - Valid Triangle Tester Prompt the user to enter in 3 points on a standard Cartesian coordinate plane. You can assume the user will enter these values as floating point numbers. Compute the distance between each of two points - so you will be computing 3 distance values. Use the distance formula to do this. d=/(x2-x2)2 + ( Y Y )2 Note that you can raise a value to the 0.5 power to compute the square root, or you can use the sqrt() function in the math module - your choice! Report the distance to the user of each side, rounded to 2 decimal places Next, determine if the three points could form a valid triangle. You can assume that the triangle is valid by checking the following: (a) Side 1 + Side 2 must be longer than Side 3 (b) Side 2 + Side 3 must be longer than Side 1 (c) Side 3 + Side 1 must be longer than Side 2 Here are some sample runnings of the program, as well as a diagram that will help you to visualize the problem: 0,100 100,100 0,0 100,0 110,100 50,50 0,0 75,25 0,0 Valid and Invalid Triangles -------- RUN #1 -------- Valid Triangle Tester Enter Point #1 - x position: 0 Enter Point #1 - y position: 0 Enter Point #2 - x position: 0 Enter Point #2 - y position: 100 Enter Point #3 - x position: 100 Enter Point #3 - y position: 0 The length of each side of your test shape is: Side 1: 100.00 Side 2: 141.42 Side 3: 100.00 This is a valid triangle! Part 4 - Valid Triangle Tester Prompt the user to enter in 3 points on a standard Cartesian coordinate plane. You can assume the user will enter these values as floating point numbers. Compute the distance between each of two points - so you will be computing 3 distance values. Use the distance formula to do this. d=/(x2-x2)2 + ( Y Y )2 Note that you can raise a value to the 0.5 power to compute the square root, or you can use the sqrt() function in the math module - your choice! Report the distance to the user of each side, rounded to 2 decimal places Next, determine if the three points could form a valid triangle. You can assume that the triangle is valid by checking the following: (a) Side 1 + Side 2 must be longer than Side 3 (b) Side 2 + Side 3 must be longer than Side 1 (c) Side 3 + Side 1 must be longer than Side 2 Here are some sample runnings of the program, as well as a diagram that will help you to visualize the problem: 0,100 100,100 0,0 100,0 110,100 50,50 0,0 75,25 0,0 Valid and Invalid Triangles -------- RUN #1 -------- Valid Triangle Tester Enter Point #1 - x position: 0 Enter Point #1 - y position: 0 Enter Point #2 - x position: 0 Enter Point #2 - y position: 100 Enter Point #3 - x position: 100 Enter Point #3 - y position: 0 The length of each side of your test shape is: Side 1: 100.00 Side 2: 141.42 Side 3: 100.00 This is a valid triangle