Write a C program that calculates an approximate value for the definite integral of a curve using each of the two methods, the rectangle rule and the trapezoidal rule.

Define these functions first:

myFunc, which calculates a single value based on the underlying function that is being integrated. It basically returns f(x) for some input value x. As an illustration, we will set myFunc to be a polynomial function f(x) = x³ - 3x² + 2. Prototype is double myFunc(double x);

calcAreaRect, which calculates the area between two endpoints a1 and b1 using the rectangle method. This function will call myFunc. Prototype is double calcAreaRect(double a1, double b1);

calcAreaTrap, which calculates the area between two endpoints a1 and b1 using the trapezoidal method. This function will call myFunc. Prototype is double calcAreaTrap(double a1, double b1);

calcIntegral, which returns the approximation value between two end points, a and b, based on either the rectangle or trapezoidal method. calcIntegral will: (1) Divide the region between a and b into num_intervals subregions. (2) Calculate the approximate value for each sub-region according to the function calcAreaRect or calcAreaTrap. (3) Sum them all up to get the final result and return it. Prototype is double calcIntegral(int method, double a, double b, int num_intervals); // method = 1 indicates rectangle method, method = 2 indicates trapezoidal method

Follow this outline of programs logic

Ask the user which method he/she would like to use to do the integration, i.e., rectangle or trapezoid, and then to specify the endpoints. Do input validation on the method.

set num_intervals = 2

while (user has not selected to quit && num_intervals 4/4 x³ + 2x for verification

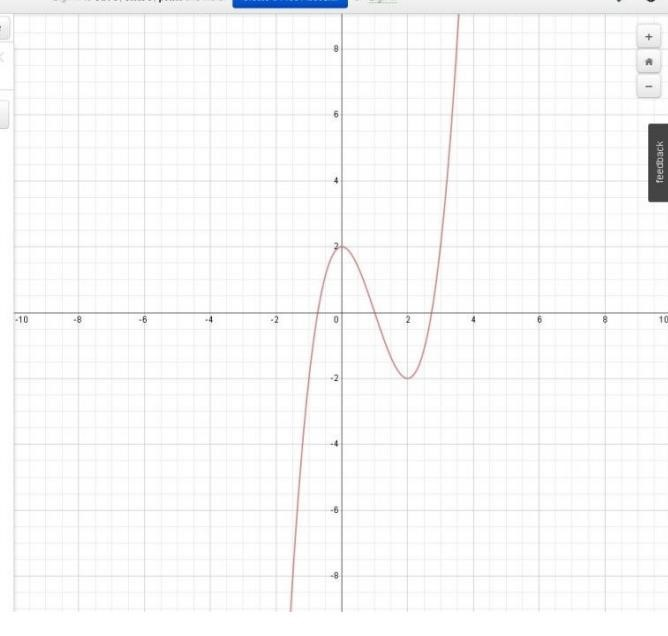
Curve of f(x) = x³ - 3x² + 2.

Examples of Output:

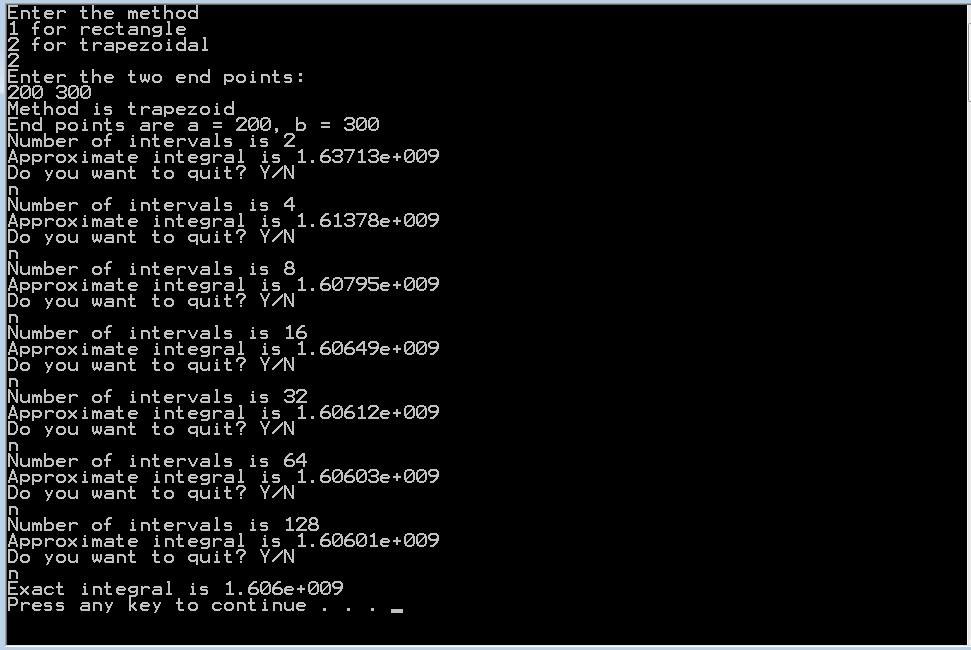
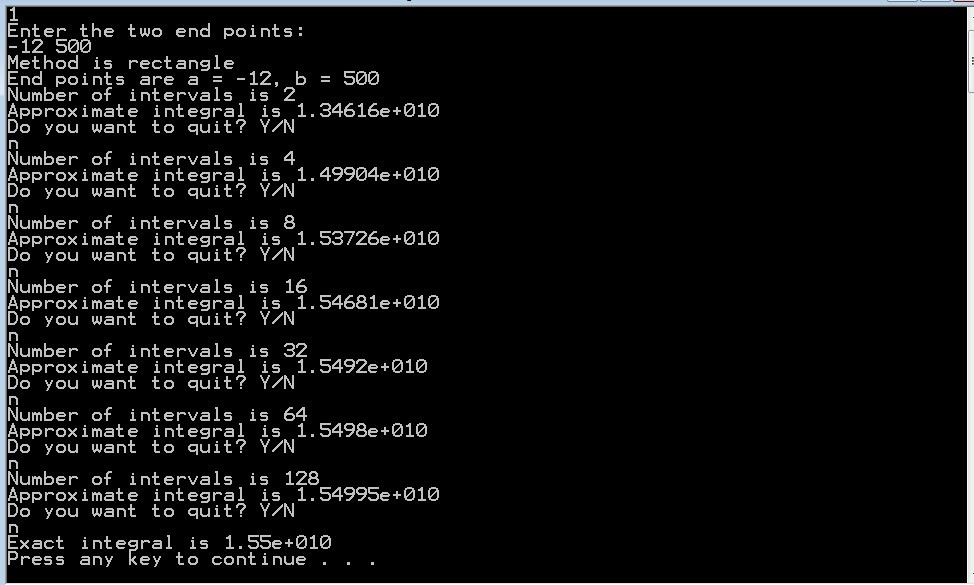
feedback