Write a function addTrees that takes two (Tree int) values and returns an (Tree int) where the corresponding nodes from the two trees are added. The trees might have different depth. You should copy particular branchesodes of the trees if the other tree doesnt have that branchode. See the example below.

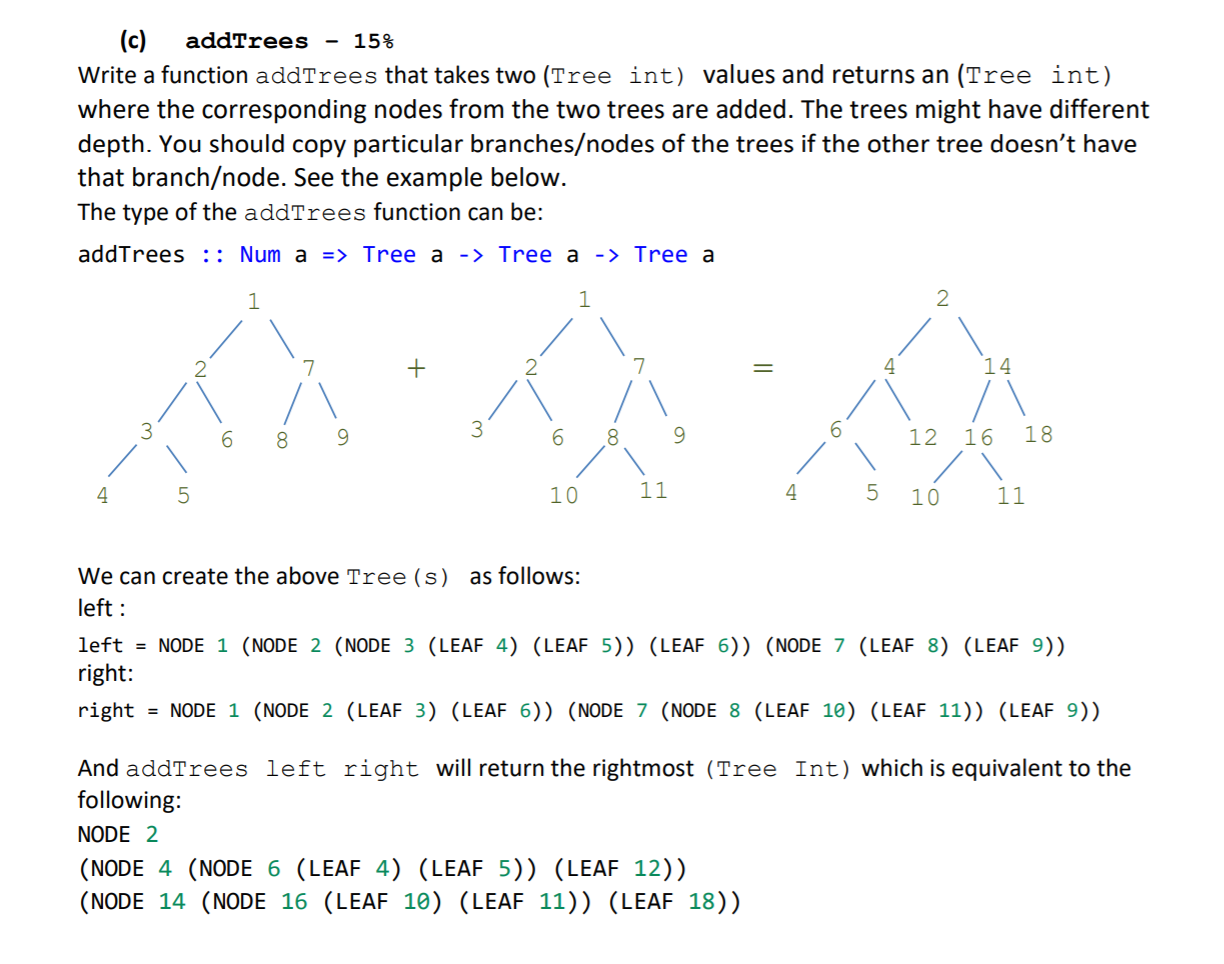
(c) addTrees - 158 Write a function addTrees that takes two (Tree int) values and returns an (Tree int) where the corresponding nodes from the two trees are added. The trees might have different depth. You should copy particular branchesodes of the trees if the other tree doesn't have that branchode. See the example below. The type of the addTrees function can be: addTrees :: Num a => Tree a -> Tree a -> Tree a i 6 & 9 1 6 8 12 16 18 4 5 11 4 5 10 11 We can create the above Tree (s) as follows: left: left = NODE 1 (NODE 2 (NODE 3 (LEAF 4) (LEAF 5)) (LEAF 6)) (NODE 7 (LEAF 8) (LEAF 9)) right: right = NODE 1 (NODE 2 (LEAF 3) (LEAF 6)) (NODE 7 (NODE 8 (LEAF 10) (LEAF 11)) (LEAF 9)) And addTrees left right will return the rightmost (Tree Int) which is equivalent to the following: NODE 2 (NODE 4 (NODE 6 (LEAF 4) (LEAF 5)) (LEAF 12)) (NODE 14 (NODE 16 (LEAF 10) (LEAF 11)) (LEAF 18)) (c) addTrees - 158 Write a function addTrees that takes two (Tree int) values and returns an (Tree int) where the corresponding nodes from the two trees are added. The trees might have different depth. You should copy particular branchesodes of the trees if the other tree doesn't have that branchode. See the example below. The type of the addTrees function can be: addTrees :: Num a => Tree a -> Tree a -> Tree a i 6 & 9 1 6 8 12 16 18 4 5 11 4 5 10 11 We can create the above Tree (s) as follows: left: left = NODE 1 (NODE 2 (NODE 3 (LEAF 4) (LEAF 5)) (LEAF 6)) (NODE 7 (LEAF 8) (LEAF 9)) right: right = NODE 1 (NODE 2 (LEAF 3) (LEAF 6)) (NODE 7 (NODE 8 (LEAF 10) (LEAF 11)) (LEAF 9)) And addTrees left right will return the rightmost (Tree Int) which is equivalent to the following: NODE 2 (NODE 4 (NODE 6 (LEAF 4) (LEAF 5)) (LEAF 12)) (NODE 14 (NODE 16 (LEAF 10) (LEAF 11)) (LEAF 18))