Write a function $($not a method$),$ closest$\_$point$\_$on$\_$line$\_$segment $($p$,$ a$,$ b$),$ which returns a Vec

object that is the closest point to vec$(p)$ on the line segment formed by vec$(a)$ and vec$(b).$ Parameters $p,$a and $b$ a

all Vec$2$D objects.

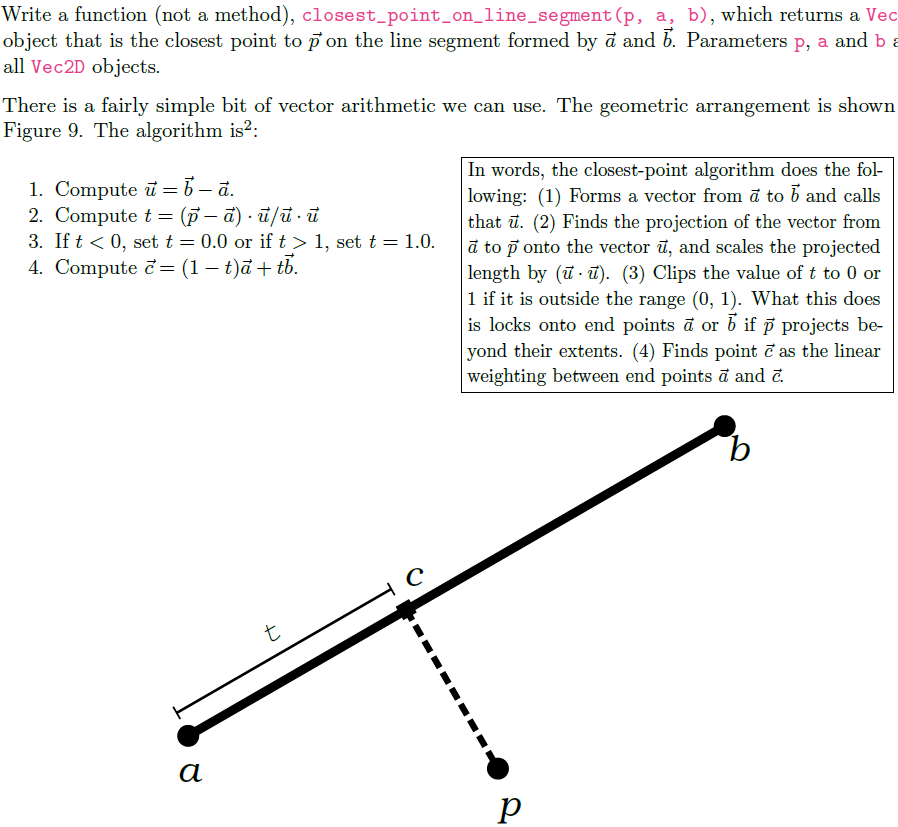
There is a fairly simple bit of vector arithmetic we can use. The geometric arrangement is shown

Figure $9.$ The algorithm is is ${?}^2$ :

Compute vec$(u)=$vec$(b)-$vec$(a).$

Compute $t=(vec(p)-$vec$(a))*vec\frac{u}{v}ec(u)*vec(u)$

If set $t=0\mathrm{.}0$ or if $t>1,$ set $t=1\mathrm{.}0.$

Compute vec$(c)=(1-t)vec(a)+$tvec$(b).$

In words, the closest$-$point algorithm does the fol$-$

lowing: $(1)$ Forms a vector from vec$(a)$ to vec$(b)$ and calls

that vec$(u).(2)$ Finds the projection of the vector from

vec$(a)$ to vec$(p)$ onto the vector vec$(u),$ and scales the projected

length by $(vec(u)*vec(u)).(3)$ Clips the value of $t$ to $0$ or

$1$ if it is outside the range $(0,1).$ What this does

is locks onto end points vec$(a)$ or vec$(b)$ if vec$(p)$ projects be$-$

yond their extents. $(4)$ Finds point vec$(c)$ as the linear

weighting between end points vec$(a)$ and vec$(c).$

Sample

$>>>$ from math import sqrt

$>>>$ a $=$ Vec$2$D$(0\mathrm{.}0,0\mathrm{.}0)$

$>>>$ b $=$ Vec$2$D$(1/$sqrt$(2),1/$sqrt$(2))$

$>>>$ p $=$ Vec$2$D$($sqrt$(0\mathrm{.}5),0\mathrm{.}0)$

$>>>$ c $=$ closest$\_$point$\_$on$\_$line$\_$segment$($p$,$ a$,$ b$)$

$>>>$ c

Vec$2$D$(0\mathrm{.}3535533905932738,0\mathrm{.}3535533905932738)$