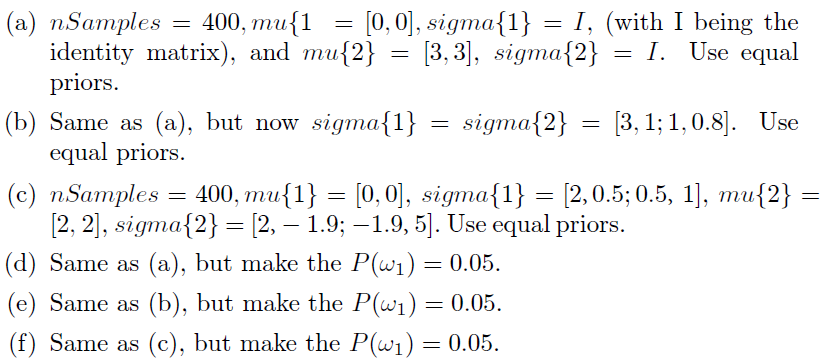
Write a function that generates independent and identically distributed samples given class-specific parameters. The class conditional densities are normal distributions accepting class dependent means and covariances The function should also accept arbitrary class priors P(wi). Be sure to test your function with some simple cases to validate that it is working correctly. Here are the specifications for the function: function [data, classIndex-generateGaussianSamples(mu, sigma, nSam- ples, prior); (a) nSanples = 400.1n u{1 identity matrix), and mus23, 3], sigma2 priors. 10.0], sigma{1} = 1, (with 1 being the I. Use equal sigma\2)- 3,1; 1,0.8]. Use ) - (b) Same as (a), but now sigmas1) equal priors (c) nSamples 400, u1[ 0.01. siqma1 2.-1.9.-1.9, 5]. Use equal priors 2 2,0.5; 0.5, 1], mu2 2. 2. sigma12} (d) Same as (a), but make the P(w)0.05. (e) Same as (b), but make the P(wi)-0.05. (f) Same as (c), but make the P(w 0.05. Write a function that generates independent and identically distributed samples given class-specific parameters. The class conditional densities are normal distributions accepting class dependent means and covariances The function should also accept arbitrary class priors P(wi). Be sure to test your function with some simple cases to validate that it is working correctly. Here are the specifications for the function: function [data, classIndex-generateGaussianSamples(mu, sigma, nSam- ples, prior); (a) nSanples = 400.1n u{1 identity matrix), and mus23, 3], sigma2 priors. 10.0], sigma{1} = 1, (with 1 being the I. Use equal sigma\2)- 3,1; 1,0.8]. Use ) - (b) Same as (a), but now sigmas1) equal priors (c) nSamples 400, u1[ 0.01. siqma1 2.-1.9.-1.9, 5]. Use equal priors 2 2,0.5; 0.5, 1], mu2 2. 2. sigma12} (d) Same as (a), but make the P(w)0.05. (e) Same as (b), but make the P(wi)-0.05. (f) Same as (c), but make the P(w 0.05