Write a Matlab code:

Background: Nonlinear systems of equations occur frequently in the characterization of chemical reactions. For example, the following chemical reactions take place in a closed system

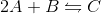
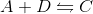
At equilibrium, they can be characterized by:

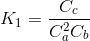
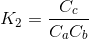
where the nomenclature ci represents the concentration of constituent i. If x1 and x2 are the number of moles of C that are produced due to the first and second reactions, respectively, formulate the equilibrium relationships as a pair of two simultaneous nonlinear equations. Then, solve the pair of simultaneous nonlinear equations for x1 and x2 if K _1= 4 x 10^4, K_2 = 3.7 x 10^-2, c_a,0= 50, c_b,0 = 20, c_c,0 = 5, and c_d,0 = 10.

Using the stoichiometry of Eqs. (8.1) and (8.2), the concentrations of each constituent can be represented in terms of x1 and x2 as

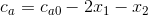
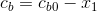
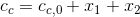
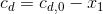
where the subscript 0 designates the initial concentration of each constituent. These values can be substituted into Eqs. (8.3) and (8.4) to give

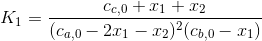
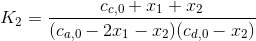
Given the parameter values, these are two nonlinear equations with two unknowns. Thus, the solution to this problem involves determining the roots of

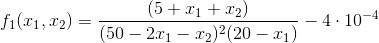
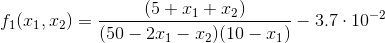
Assignment: Write a function that solve for the nonlinear equations using the Newton-Raphson method. For this assignment, you may not use symbolics. Instead, obtain the Jacobian matrix numerically, as stated above, by using the modified secant method described in Section 6.3 to calculate the derivatives in the Jacobian. You may not use any built-in Matlab functions to solve for the Jacobian. You may use the left division or the functions from your previously assignments on matrix inverse or Gauss elimination functions. The nonlinear functions should be an input in the form of f = [f1(x); f2(x); ...]; in which x = [x1; x2; x3 ...]; e.g. the functions f1 = x1^2 +x2^2 -10 = 0; f2 = x2 +3x1*x2^2 - 57 = 0 defined by using anonymous function has the following form:

f =@(x) [x(1)^2+x(2)^2-10; x(2)+3*x(1)*x(2)^2-57];

Write your nonlinear equation solver to solve for any function f, not only the nonlinear equations defined in this problem; i.e. the function, f, should be an input. If you define f by using an m file, then the input name (the handle) needs to be @f. The independent variable array, x, should have an undefined number of variables. In the example above, f contains two equations and two unknowns. Write a code that follows the following format:

function [ x, iter ] = myNL( f, xo, ea, maxit )

% nonlinear equation solver

% f = column array of m nonlinear functions (anonymous or m file)

% xo = initial guess of solution

% ea = maximum approximate error

% maxit = maximum number of iterations

% x = array of solution of nonlinear equations

% iter = the number iterations for the solution to converge to ea

end

% end of function

2A + BSC 2A + BSC