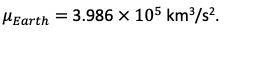
Write a MATLAB script that: MATLAB a) takes as input i. A position vector (in km) and a velocity vector (in km/s) in ECI (Earth-Centered Inertial) coordinates. ii. An initial time, t iii. A later time, tz iv. Tolerances Ar (relative tolerance) and 4A (absolute tolerance) for the iterative procedure used to solve Kepler's time equation (you may use any of the iteration schemes that we discussed in class - DO NOT use any of the built-in iterators/solvers available in MATLAB, Mathematica, etc.). b) Outputs the input data, with labels and units, and calculates the following: c) Classical orbital elements a, e, i, w, and 1 (Note that these are 5 of the 6 COES). d) The DCM CEP that converts from ECI to perifocal coordinates. e) Position (in km) and velocity (in km/s) vectors in perifocal coordinates at time t f) True and eccentric anomalies 0, and E, (in rad) at time t. g) Time of periapsis passage, To (in seconds) h) True and eccentric anomalies 62 and Ez (in rad) at time tz. i) Position (in km) and velocity (in km/s) vectors in perifocal coordinates at time tz. j) Position (in km) and velocity (in km/s) vectors in Ecl coordinates at time tz. k) Outputs the values in items (c) - 0) with labels and units. Run the program with the input values: = 6210.22 i +5963.369 2998.97 (km) = -4.25589 I +3.14487 ) - 4.45999 (km/s) t = 0 t2 = 2 hours AR = 10-6 4A = 10-6 Include a copy of all your m-files and outputs. Hearth = 3.986 x 105 km?/s. Write a MATLAB script that: MATLAB a) takes as input i. A position vector (in km) and a velocity vector (in km/s) in ECI (Earth-Centered Inertial) coordinates. ii. An initial time, t iii. A later time, tz iv. Tolerances Ar (relative tolerance) and 4A (absolute tolerance) for the iterative procedure used to solve Kepler's time equation (you may use any of the iteration schemes that we discussed in class - DO NOT use any of the built-in iterators/solvers available in MATLAB, Mathematica, etc.). b) Outputs the input data, with labels and units, and calculates the following: c) Classical orbital elements a, e, i, w, and 1 (Note that these are 5 of the 6 COES). d) The DCM CEP that converts from ECI to perifocal coordinates. e) Position (in km) and velocity (in km/s) vectors in perifocal coordinates at time t f) True and eccentric anomalies 0, and E, (in rad) at time t. g) Time of periapsis passage, To (in seconds) h) True and eccentric anomalies 62 and Ez (in rad) at time tz. i) Position (in km) and velocity (in km/s) vectors in perifocal coordinates at time tz. j) Position (in km) and velocity (in km/s) vectors in Ecl coordinates at time tz. k) Outputs the values in items (c) - 0) with labels and units. Run the program with the input values: = 6210.22 i +5963.369 2998.97 (km) = -4.25589 I +3.14487 ) - 4.45999 (km/s) t = 0 t2 = 2 hours AR = 10-6 4A = 10-6 Include a copy of all your m-files and outputs. Hearth = 3.986 x 105 km?/s