Write a program that (1) accepts an input set of strings on lower case English letters and create a Non-deterministic Finite State Automaton (NFSA) for accepting only that set, and (2) creates an equivalent Deterministic Finite State Automaton (DFSA) corresponding to the NFSA using the subset construction algorithm. (Program in Java please thanks!)

Example:

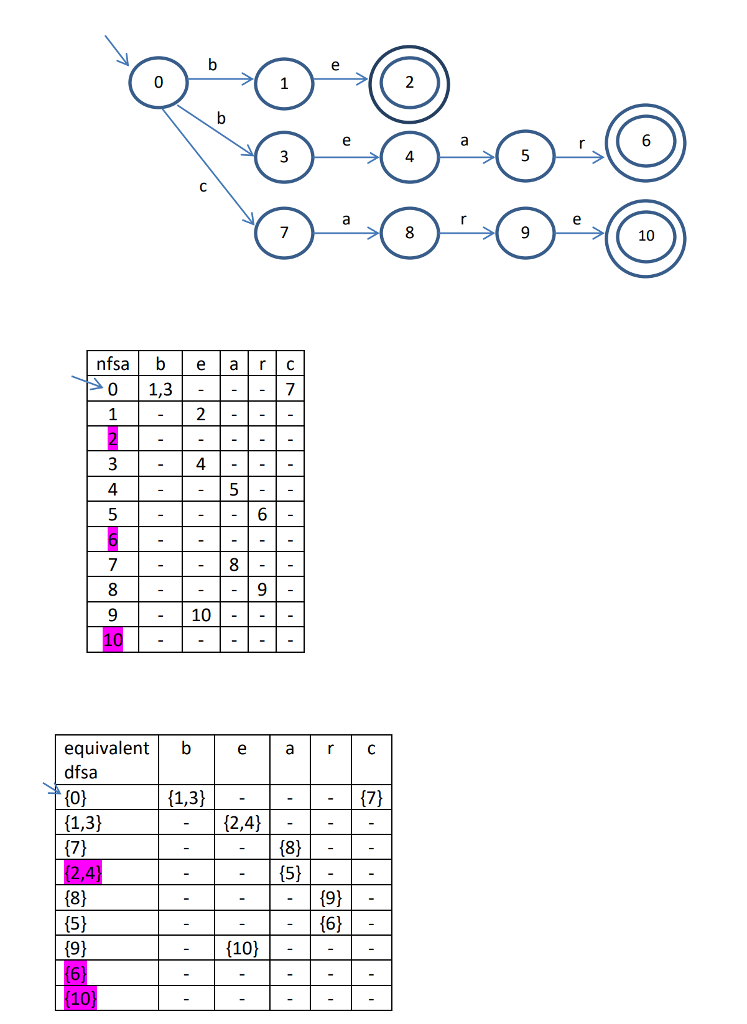
Write a program that (1) accepts an input set of strings on lower case English letters and create a Non-deterministic Finite State Automaton (NFSA) for accepting only that set, and (2) creates an equivalent Deterministic Finite State Automaton (DFSA) corresponding to the NFS A using the subset construction algorithm covered in class Sample input: be state 4: r 6 state 5: r7 state 6: e 8 state 7: none state 8: none Sample output of phase 1-NFSA: (1) number of states: 11 (2) final states: 2, 6, 10 (3) alphabet: abedefghijklm nopqrstuvwxyz (4) transitions: (4) test strings Reject be 0 c 7 cars 8 r 9 Reject with the follo Sample output of phase 2- The equivalent DFSA: (1) number of states:9 (1) A language contains (be, bear, care. Test strings: care, b, be, bea, bears, bear, cars car, c, beare. state 0: O state 1: 1 3 state 2: (7) state 3: 2 4) state 4: (8 state 5: 15 state 6: 9 state 7: 6) state 8: 0 (2) A language contains program, procedure, proceed. Test strings: &, prog, program, procram, procedures, proceed, procee, procedure, procedurr, noprocedure. (3) A language contains (do, double, throw, throws, int, interface, final, finally). Test strings: finall, inter, throws, does, do, int, final, throwthrows, interface, int double. (2) final states: 3, 7, 8 (3) transitions: state 0: b1, c 2 state 1: e 3 state 2: a 4 state 3: a 5 Write a program that (1) accepts an input set of strings on lower case English letters and create a Non-deterministic Finite State Automaton (NFSA) for accepting only that set, and (2) creates an equivalent Deterministic Finite State Automaton (DFSA) corresponding to the NFS A using the subset construction algorithm covered in class Sample input: be state 4: r 6 state 5: r7 state 6: e 8 state 7: none state 8: none Sample output of phase 1-NFSA: (1) number of states: 11 (2) final states: 2, 6, 10 (3) alphabet: abedefghijklm nopqrstuvwxyz (4) transitions: (4) test strings Reject be 0 c 7 cars 8 r 9 Reject with the follo Sample output of phase 2- The equivalent DFSA: (1) number of states:9 (1) A language contains (be, bear, care. Test strings: care, b, be, bea, bears, bear, cars car, c, beare. state 0: O state 1: 1 3 state 2: (7) state 3: 2 4) state 4: (8 state 5: 15 state 6: 9 state 7: 6) state 8: 0 (2) A language contains program, procedure, proceed. Test strings: &, prog, program, procram, procedures, proceed, procee, procedure, procedurr, noprocedure. (3) A language contains (do, double, throw, throws, int, interface, final, finally). Test strings: finall, inter, throws, does, do, int, final, throwthrows, interface, int double. (2) final states: 3, 7, 8 (3) transitions: state 0: b1, c 2 state 1: e 3 state 2: a 4 state 3: a 5