Write a program that uses these bounds and bisection search to find the smallest monthly payment to the cent (no more multiples of $10) such that we can pay off the debt within a year.

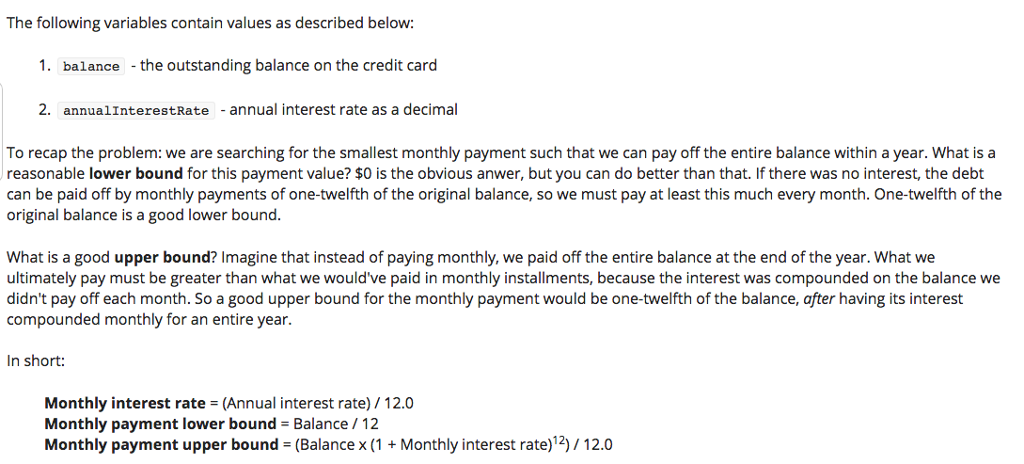
The following variables contain values as described below: 1. balance the outstanding balance on the credit card 2. annual InterestRate annual interest rate as a decima To recap the problem: we are searching for the smallest monthly payment such that we can pay off the entire balance within a year. What is a reasonable lower bound for this payment value? $0 is the obvious anwer, but you can do better than that. If there was no interest, the debt can be paid off by monthly payments of one-twelfth of the original balance, so we must pay at least this much every month. One-twelfth of the original balance is a good lower bound What is a good upper bound? Imagine that instead of paying monthly, we paid off the entire balance at the end of the year. What we ultimately pay must be greater than what we would've paid in monthly installments, because the interest was compounded on the balance we didn't pay off each month. So a good upper bound for the monthly payment would be one-twelfth of the balance, after having its interest compounded monthly for an entire year. In short: Monthly interest rate -(Annual interest rate) 12.0 Monthly payment lower bound Balance 12 Monthly payment upper bound Balance x (1 Monthly interest rate) 12 12.0