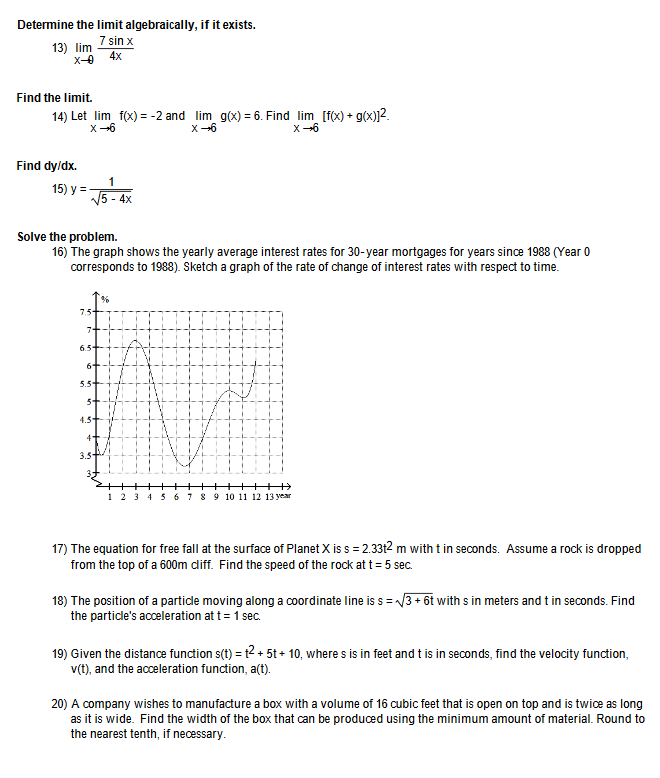
Write an equation for the line described. 1) Passes through (5, -1) and perpendicular to the line -7x + 8y = -43 A) y = - 8X + 33 8 B) y= - =X C) y =X+ 33 33 7 D) y = - =X+ 7 Find the limit, if it exists. 2) lim x2 + 3x + 19 X-z x3 + 2x2 + 10 19 A) 10 B) 1 C) 0 D) 3) lim 2-x + x-1 X-z 4x + -2 A) x C) D) 0Find the vertical asymptotes of the graph of f(x). 4) f(x) = 1 (x - 9) A) X = -9 B) x = 1 C) no vertical asymptotes D) x =9 Find the slope of the line tangent to the curve at the given value of x. 5) f(x) = - 10x2 + 8x; x =9 A) -108 B) -243 C) - 140 D) -172 Find the intervals on which the function is continuous. 6) y = 10x - 10 A) [- 1, =) B) [1, 20) C) (1, 30) D) (- 2, 1] Find dy/dx. 7) s = t3 - cact + 17 A) 3t- - cact cot t B) t2 - cot2t + 17 C) 3t2 + cot2t D) 312 + cact cot t Find dy/dx by implicit differentiation. If applicable, express the result in terms of x and y. 8) 9y + -8xy - 7 = 0 By A) 9 + -8xy B) By(x + 1) By 9 C 9+ -8x D) 8(x + y) 9 Determine the limit algebraically, if it exists. 9) x2 + 11x + 10 X-10 X + 10 A) -9 B) 11 C) 220 D) Does not exist Determine the limit graphically, if it exists. 10) lim f(x) X-1/2 F(x) A) Does not exist B) 0 C) - 1 D) -2 SHORT ANSWER. You must show all your work to receive full credit. A particle moves from A to B in the coordinate plane. Find the increments Ax and Ay in the particle's coordinates. 11) A(-10, -6), B(-3, -2) Determine if the function is even, odd, or neither. 12) y = \\x2 - 3Determine the limit algebraically, if it exists. 13) lim - 7 sin x X-0 4X Find the limit. 14) Let lim f(xx) = -2 and lim g(x) =6. Find lim [f() + g(x)]2. X -6 g- X 9- x Find dy/dx. 15) y = 5 - 4x Solve the problem. 16) The graph shows the yearly average interest rates for 30-year mortgages for years since 1988 (Year 0 corresponds to 1988). Sketch a graph of the rate of change of interest rates with respect to time. 75 6.5- 64 5.5- 4.5- 3.5- 17) The equation for free fall at the surface of Planet X is s = 2.33t- m with t in seconds. Assume a rock is dropped from the top of a 600m cliff. Find the speed of the rock at t = 5 sec 18) The position of a particle moving along a coordinate line is s = 3 + 6t with s in meters and t in seconds. Find the particle's acceleration at t = 1 sec. 19) Given the distance function s(t) = t