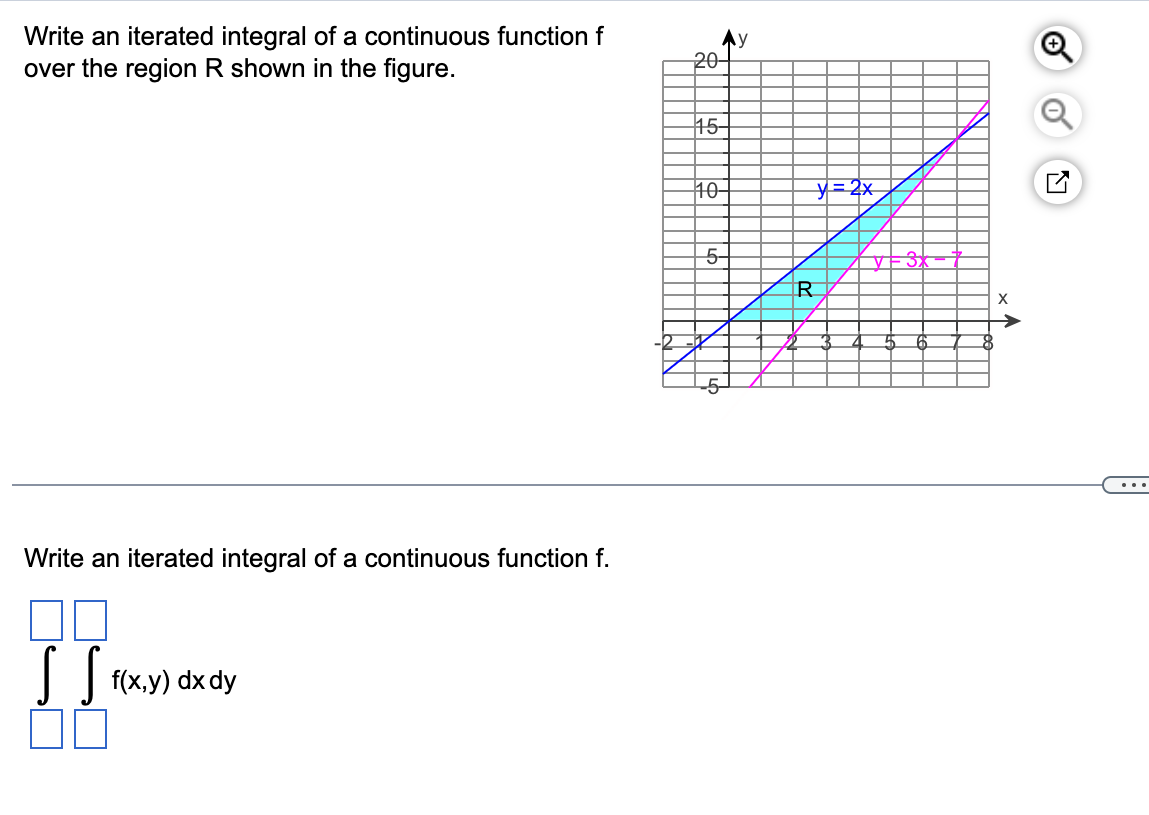
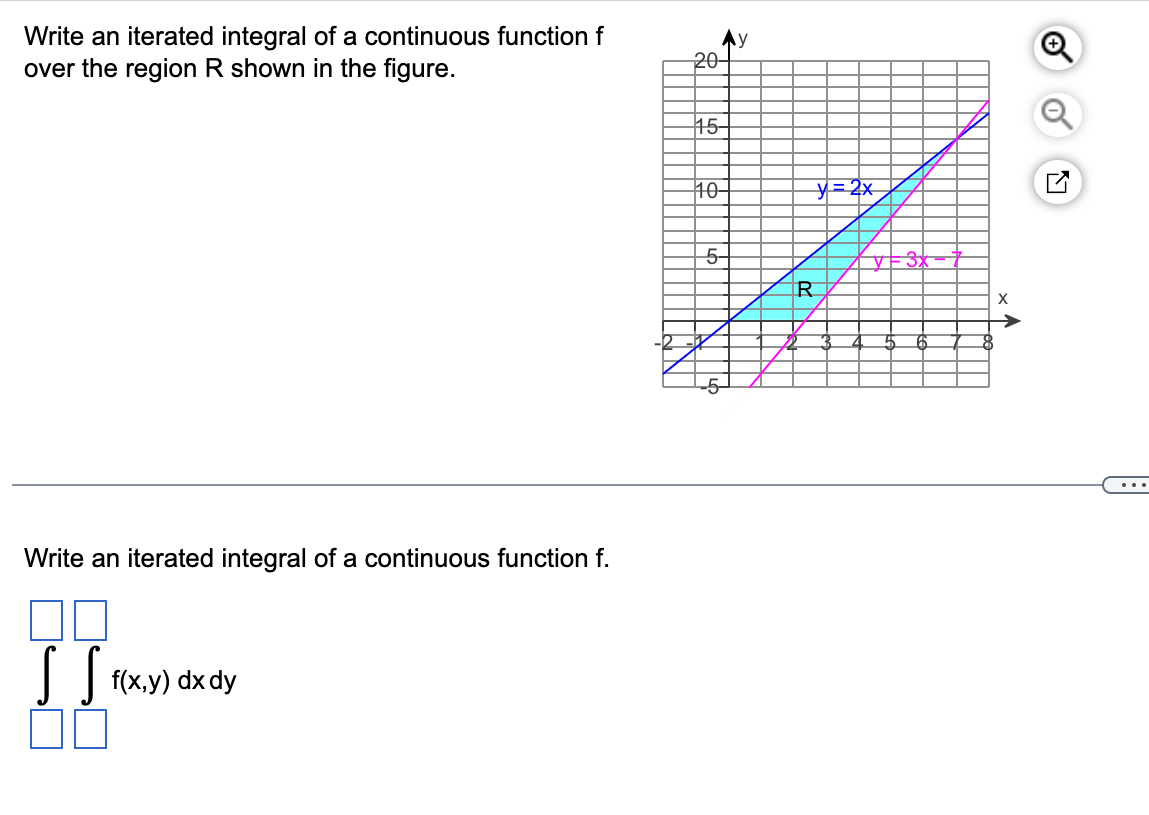
Question: Write an iterated integral of a continuous function f over the region R shown in the figure. + 15 10- y= 2 x 5 -




![4x R X .. Reverse the order of integration. 70 [ ]](https://s3.amazonaws.com/si.experts.images/answers/2024/06/66639fada33f2_97366639fad83da0.jpg)

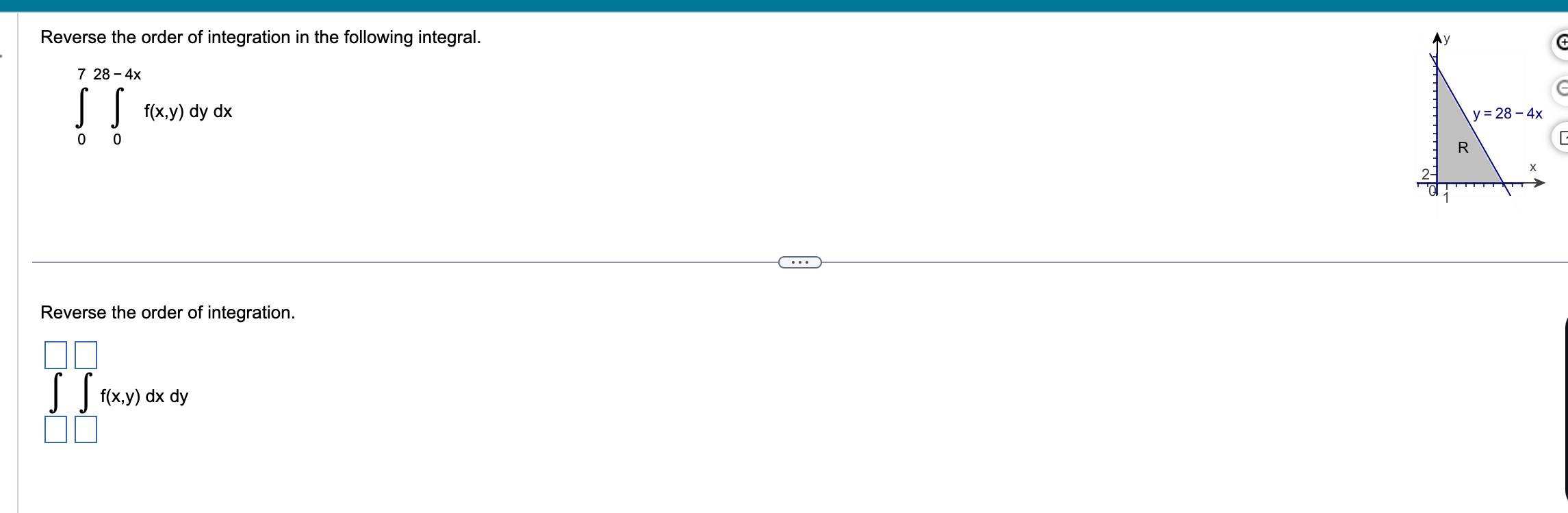


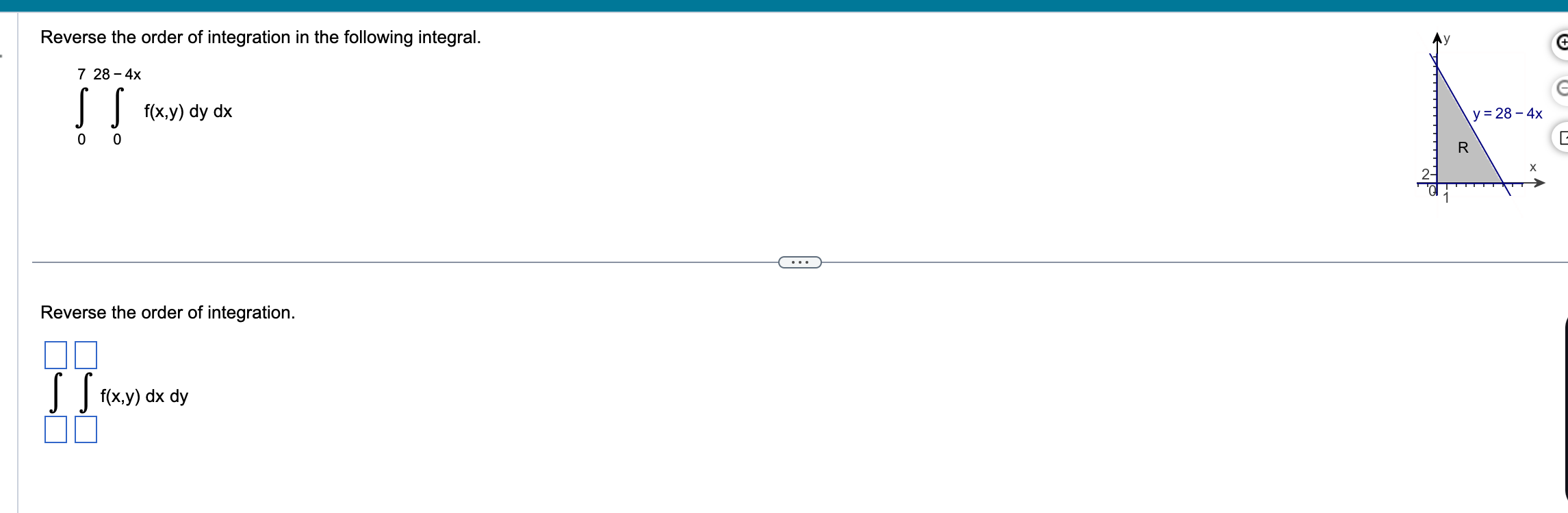
Write an iterated integral of a continuous function f over the region R shown in the figure. + 15 10- y= 2 x 5 - R X . . Write an iterated integral of a continuous function f. f(x,y) dx dy\fEvaluate the following integral, where R is bounded by x = 3, y = 3x + 6, and y = - x - 2. dA R SS 12 dA = (Simplify your answer.) RReverse the order of integration in the following integral. 7 28 - 4x J f(x,y) dy dx o y = 28 - 4x R X .. Reverse the order of integration. 70 [ ] fx,y) dx dy 00Reverse the order of integration and evaluate the following integral. 2e dx dy y dx dy = y (Type an exact answer in terms of e.)Use double integrals to compute the area of the region bounded by the parabola y = 3x2 and the line y = 27. units. square units. cubic units. Find the volume of the following solid. Z 4xy+z= 30 The solid above the region R =((x,y): 0 S x 5 3,0 5 y S 6 - x} and between the planes - 5x - 5y+ z = 0 and - 4x - y+ z = 30 The volume of the solid is V (Type an integer or a simplied fraction.)
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


