write code by """"OCTAVE""""" same form of newton method

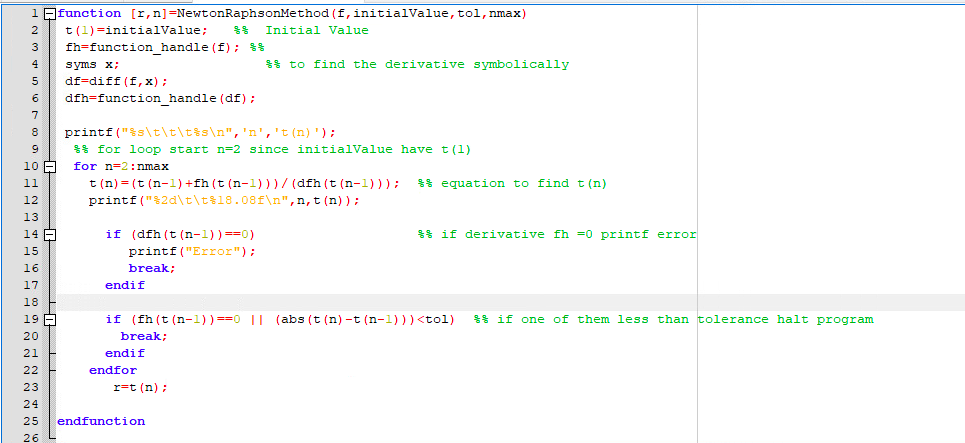
2.3.1 The Secant Method To avoid the issue with the computation of the derivative in the Newton-Raphson Method, an alternative method called the Secant Method can be used. In this method, we simply approximate f'(xn-1) with f(xn-1) - f(xn-2) 2n-1 Xn-2 which leads to the iteration equation f(In-1)(xn-1 Xn-2) In = {n-1- f(In-1) - f(xn-2) For this algorithm we will need two initial values. Further, we will not need to differentiate so we won't use the variable dfh and we won't need to type syms x in the m-file. MO 1 Q function (r, n] =NewtonRaphsonMethod(f, initialValue, tol, nmax) t(1)=initialValue; $$ Initial Value fh=function_handle(f); $$ syms x; $$ to find the derivative symbolically df=diff(f,x); dfh=function_handle (df); 10 11 printf("%s\t\t\tss ", 'n','t (n)'); *% for loop start n=2 since initialValue have t(1) for n=2 : nmax t(n)=(t (n-1) +fh (t (n-1)))/(dfh (t (n-1))); $$ equation to find tan) printf("%d\t\t$18.08 ", n, t(n)); 1 *$ if derivative fh =0 printf error if (dfh(t (n-1))==0) printf("Error"); break; endif $$ if one of them less than tolerance halt program ET if (fh(t (n-1))==0 || (abs(t (n)-t (n-1)))