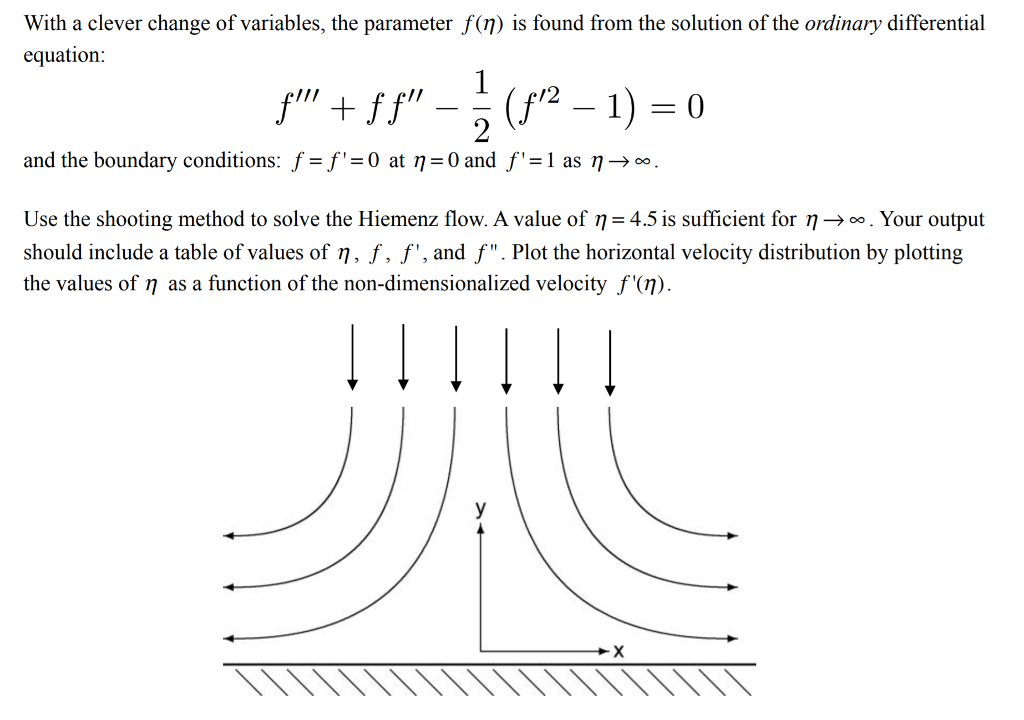
Question: Write code using MatLab (25 pts) The description of the laminar boundary layer in flow in a stagnation plane is a classical boundary value problem

Write code using MatLab
(25 pts) The description of the laminar boundary layer in flow in a stagnation plane is a classical boundary value problem and is called Hiemenz flow. This is an example of plane potential flow that arrives from the y-axis and impinges on a flat wall placed at y-0, divides into two streams on the wall, and leaves in both directions. The viscous interaction with the wal influences the velocity distribution in the neighborhood of the stagnation point and has profound influence on the momentum of the fluid. This problem has relevant applications in the study of fluid jets and welding flows. 3. The solution is obtained from the non-linear partial differential equations reduced from the famous Navier Stokes equations. The horizontal velocity distribution is given by u = U, ' where 110 is the free-stream velocity. The parameter f (7) is non-dimensional and is a function of the geometric coordinates x and y (25 pts) The description of the laminar boundary layer in flow in a stagnation plane is a classical boundary value problem and is called Hiemenz flow. This is an example of plane potential flow that arrives from the y-axis and impinges on a flat wall placed at y-0, divides into two streams on the wall, and leaves in both directions. The viscous interaction with the wal influences the velocity distribution in the neighborhood of the stagnation point and has profound influence on the momentum of the fluid. This problem has relevant applications in the study of fluid jets and welding flows. 3. The solution is obtained from the non-linear partial differential equations reduced from the famous Navier Stokes equations. The horizontal velocity distribution is given by u = U, ' where 110 is the free-stream velocity. The parameter f (7) is non-dimensional and is a function of the geometric coordinates x and y
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


