Question: Write in Python the following functions related to RSA: Exponentiation: Return the table of powers of 2 for a given number (see Appendix 2). Appendix
Write in Python the following functions related to RSA:
Exponentiation: Return the table of powers of 2 for a given number (see Appendix 2).
Appendix 2. RSA implementation. Example.
Consider this table of powers of 855:
855^1 = 855 (mod 3233) 855^2 = 367 (mod 3233) 855^4 = 367^2 (mod 3233) = 2136 (mod 3233) 855^8 = 2136^2 (mod 3233) = 733 (mod 3233) 855^16 = 733^2 (mod 3233) = 611 (mod 3233) 855^32 = 611^2 (mod 3233) = 1526 (mod 3233) 855^64 = 1526^2 (mod 3233) = 916 (mod 3233) 855^128 = 916^2 (mod 3233) = 1709 (mod 3233) 855^256 = 1709^2 (mod 3233) = 1282 (mod 3233) 855^512 = 1282^2 (mod 3233) = 1160 (mod 3233) 855^1024 = 1160^2 (mod 3233) = 672 (mod 3233) 855^2048 = 672^2 (mod 3233) = 2197 (mod 3233)
Given the above, we know this:
855^2753 (mod 3233) =855^(1+64 +128+512+2048)(mod3233)
5
= 855^1 * 855^64 * 855^128 * 855^512 * 855^2048 (mod 3233) = 855 * 916 * 1709 * 1160 * 2197 (mod 3233) = 794 * 1709 * 1160 * 2197 (mod 3233) = 2319 * 1160 * 2197 (mod 3233)
= 184 * 2197 (mod 3233) = 123 (mod 3233) = 123
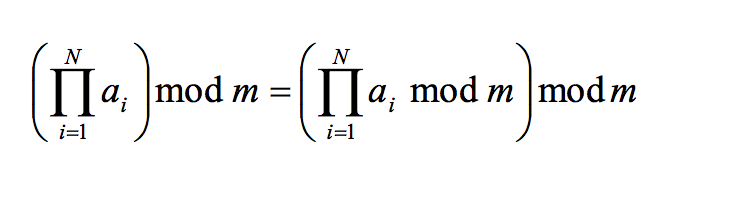
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


