write pseudocode

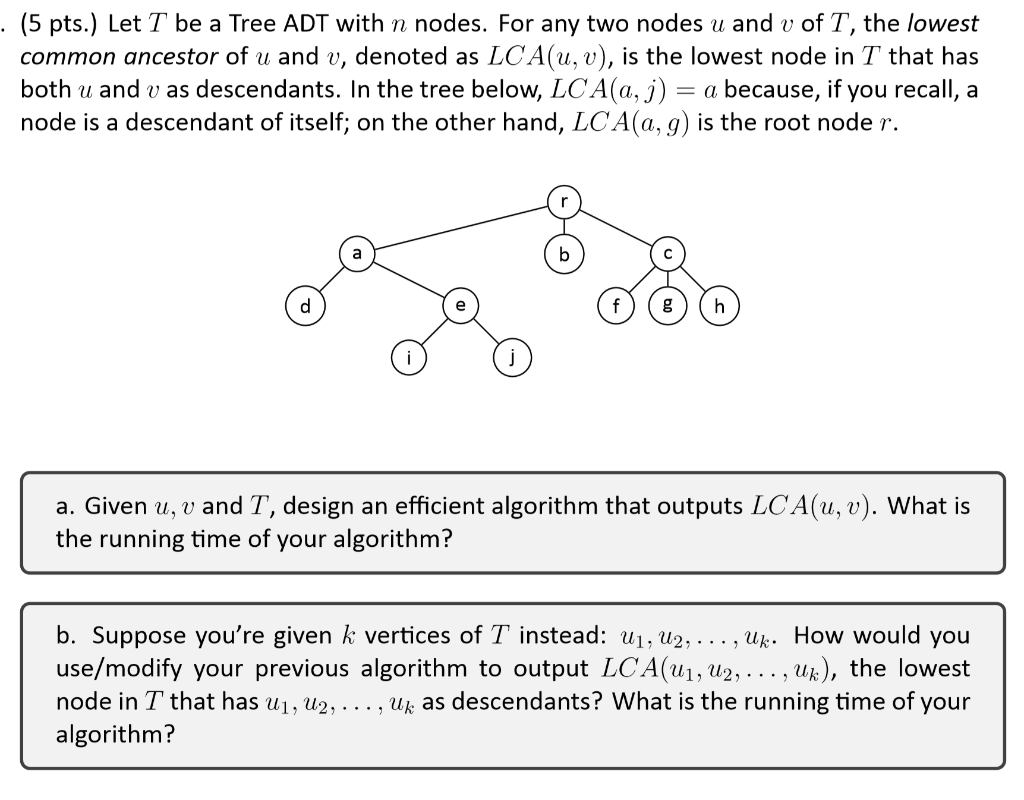
. (5 pts.) Let T be a Tree ADT with n nodes. For any two nodes u and v of T, the lowest common ancestor of u and v, denoted as LC A(u, v), is the lowest node in T that has both u and v as descendants. In the tree below, LC A(a,j) = a because, if you recall, a node is a descendant of itself; on the other hand, LC A(a, g) is the root node r. a. Given u, v and T, design an efficient algorithm that outputs LCA(u, v). What is the running time of your algorithm? b. Suppose you're given k vertices of T instead: 41, U2, ..., Uk. How would you use/modify your previous algorithm to output LC A(U1, U2, ..., uk), the lowest node in T that has u1, U2, ..., Uk as descendants? What is the running time of your algorithm? . (5 pts.) Let T be a Tree ADT with n nodes. For any two nodes u and v of T, the lowest common ancestor of u and v, denoted as LC A(u, v), is the lowest node in T that has both u and v as descendants. In the tree below, LC A(a,j) = a because, if you recall, a node is a descendant of itself; on the other hand, LC A(a, g) is the root node r. a. Given u, v and T, design an efficient algorithm that outputs LCA(u, v). What is the running time of your algorithm? b. Suppose you're given k vertices of T instead: 41, U2, ..., Uk. How would you use/modify your previous algorithm to output LC A(U1, U2, ..., uk), the lowest node in T that has u1, U2, ..., Uk as descendants? What is the running time of your algorithm