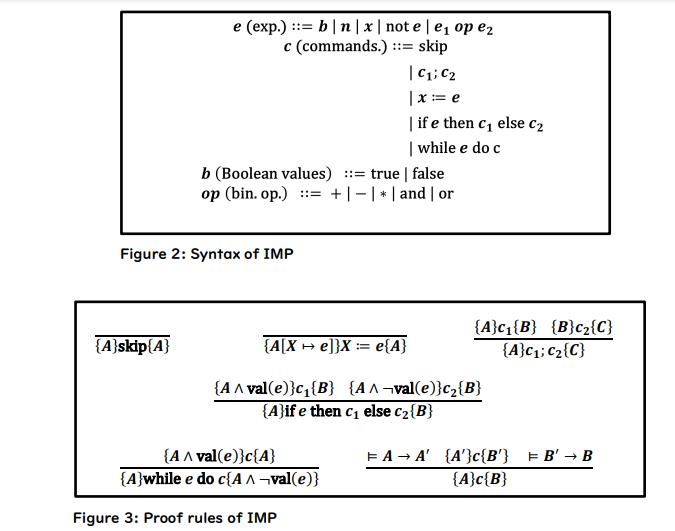
Write some program c in IMP and prove a (non-trivial) property {A}c{B} of the program by using the Hoare logic of IMP. The program must have at least one while-loop. The syntax and the proof rules of IMP are shown in Figures 2 and 3, respectively. e (exp.) : b|n| x | note | e op ez c (commands.) ::= skip C; C2 |x == e | if e then c else C | while e do c {A}skip{A} b (Boolean values) ::= true | false op (bin. op.) ::= +|- |* and | or Figure 2: Syntax of IMP {A[Xe]}X = e{A} {A A val(e)}c {B} {AA-val(e)}c{B} {A}ife then c else c {B} {A A val(e)}c{A} {A}while e do c{A A val(e)} {A}c{B} {B}c{C} {A}C; C {C} Figure 3: Proof rules of IMP FAA' {A} c{B'} EB' B {A}c{B}