Write the code for (Java) a decrease-by-one minimal change algorithm to generate all permutations of numbers {1,2,,n}. User inputs positive integer n and program generates permutations of {1,2,,n}. Provide code, and resulting permutations for the following two tests ( inputs n=3 and n=5.)

This is how it should work:

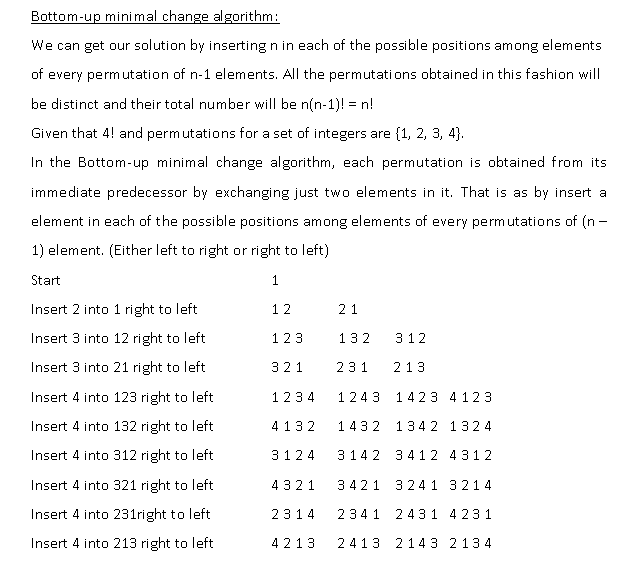
Bottom-up minimal change algorithm We can get our solution by inserting nin each of the possible positions among elements of every permutation of n-1 elements. All the permutations obtained in this fashion will be distinct and their total number will be n(n-1)! 3n! Given that 4! and permutations for a set of integers are 11, 2, 3, 4. In the Bottom-up minimal change algorithm, each permutation is obtained from its immediate predecessor by exchanging just two elements in it. That is as by insert a element in each of the possible positions among elements of every permutations of (n 1) element. (Either left to right or right to left) Start Insert 2 into 1 right to left 1 2 21 1 2 3 1 3 2 1 2 Insert 3 into 12 right to left Insert 3 into 21 right to left 3 2 1 3 1 2 1 3 1 2 3 4 124 3 1 4 2 3 4 1 2 3 Insert 4 into 123 right to left 4 1 3 2 1 4 3 2 1 3 4 2 1 3 2 4 Insert 4 into 132 right to left Insert 4 into 312 right to left 3 1 2 4 3 1 4 2 3 4 1 2 4 3 1 2 Insert 4 into 321 right to left 4 3 2 1 3 4 2 1 3 2 4 1 3 2 1 4 Insert 4 into 231right to left 2 3 1 4 2 3 4 1 2 4 3 1 4 2 3 1 Insert 4 into 213 right to left 4 2 1 3 2 4 1 3 21 4 3 2 1 3 4 Bottom-up minimal change algorithm We can get our solution by inserting nin each of the possible positions among elements of every permutation of n-1 elements. All the permutations obtained in this fashion will be distinct and their total number will be n(n-1)! 3n! Given that 4! and permutations for a set of integers are 11, 2, 3, 4. In the Bottom-up minimal change algorithm, each permutation is obtained from its immediate predecessor by exchanging just two elements in it. That is as by insert a element in each of the possible positions among elements of every permutations of (n 1) element. (Either left to right or right to left) Start Insert 2 into 1 right to left 1 2 21 1 2 3 1 3 2 1 2 Insert 3 into 12 right to left Insert 3 into 21 right to left 3 2 1 3 1 2 1 3 1 2 3 4 124 3 1 4 2 3 4 1 2 3 Insert 4 into 123 right to left 4 1 3 2 1 4 3 2 1 3 4 2 1 3 2 4 Insert 4 into 132 right to left Insert 4 into 312 right to left 3 1 2 4 3 1 4 2 3 4 1 2 4 3 1 2 Insert 4 into 321 right to left 4 3 2 1 3 4 2 1 3 2 4 1 3 2 1 4 Insert 4 into 231right to left 2 3 1 4 2 3 4 1 2 4 3 1 4 2 3 1 Insert 4 into 213 right to left 4 2 1 3 2 4 1 3 21 4 3 2 1 3 4