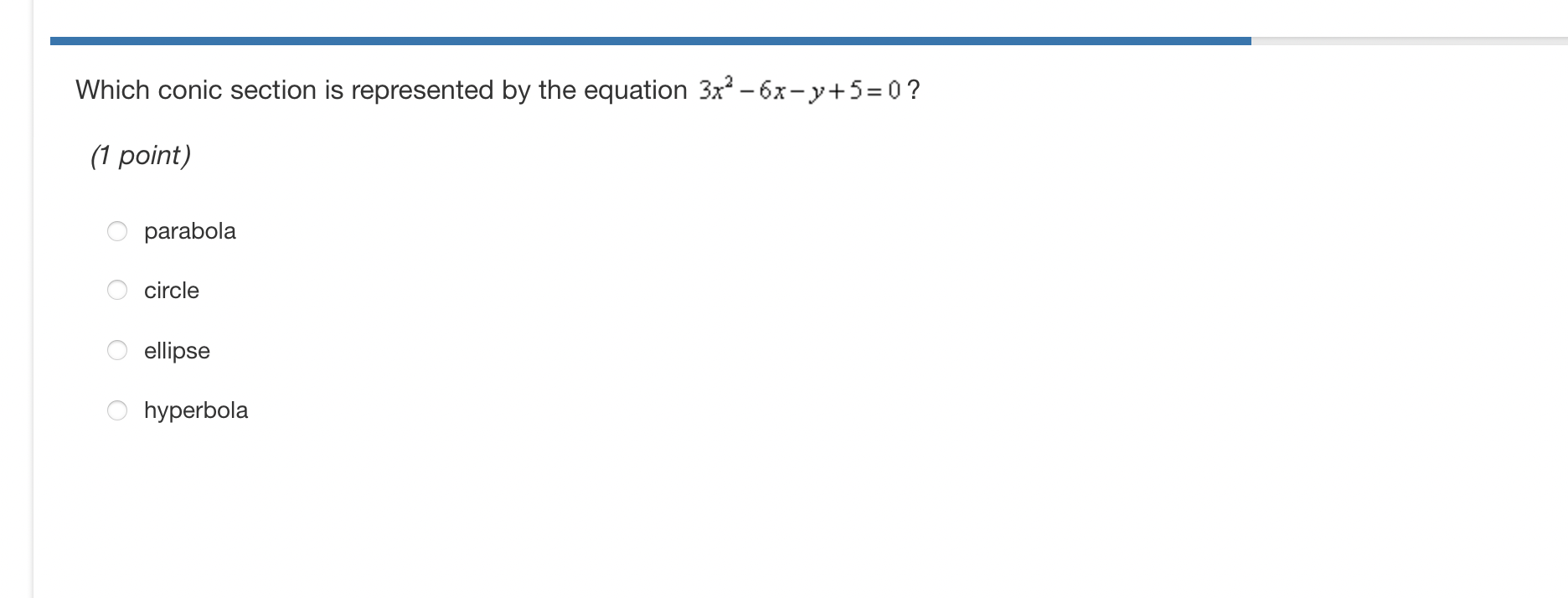
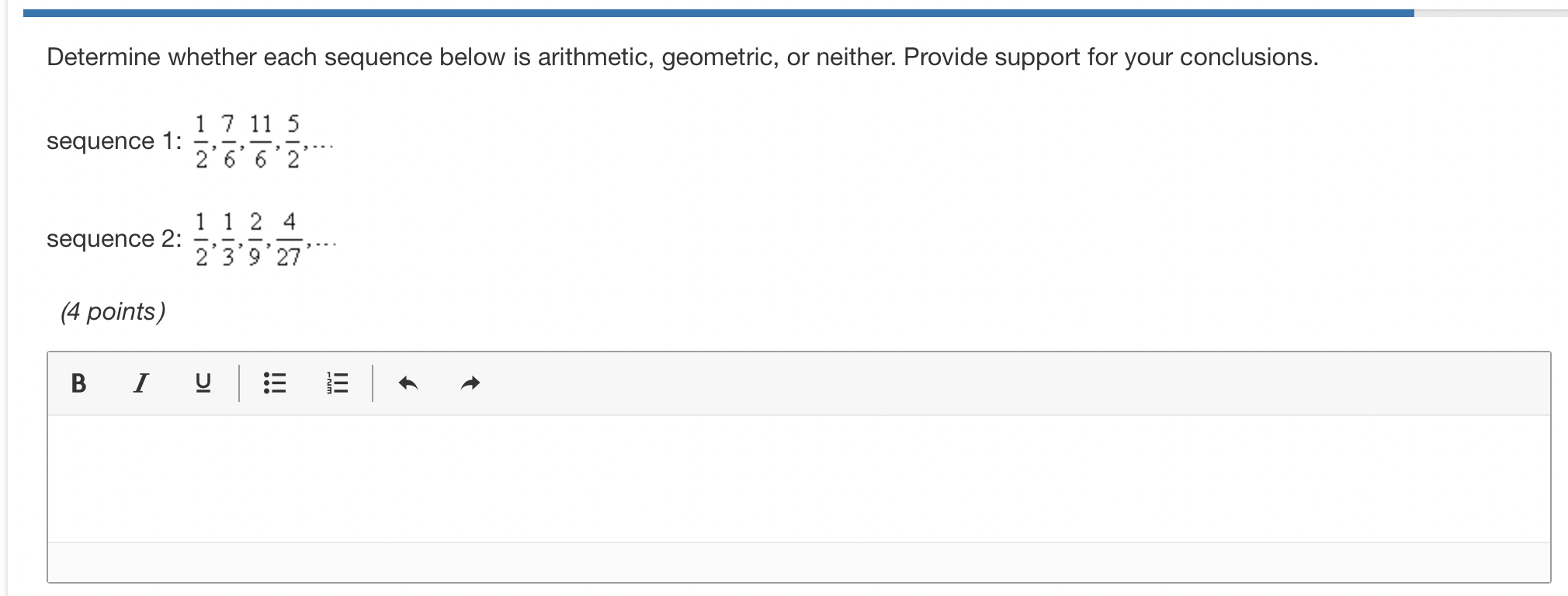
Write the expression as a single logarithm. 15 -log(x+ y)-log(x->) (1 point) O log (x+ y)3 (x - y)s O log (xty) (x-y)3 O - log(x+y) -1 O log(x+y)2Find the zero or zeroes of the function f (x) =log, (3x + 2) +log, (x -3) . (1 point) 7+ 133 O X= 6 7+ V133 O X= 6 O X= -2 and x = 3 W O X = 3Identify the focus and directrix of the parabola represented by the equation (y - 2) = 4(x+ 2). (1 point) The focus is (-3,2) and the directrix is x = -1. The focus is (-2,2) and the directrix is x = -1. The focus is (2,-2) and the directrix is y = -1. O The focus is (2,-3) and the directrix is y = -1.Which conic section is represented by the equation 3;:2 6xy+ 5 = 0 ? (1 point) parabola circle ellipse hyperbola 2 2 What are the vertices of the hyperbola given by 02) _ (\"6) =1? 25 9 (1 point) (0,2) and(10,2) (12) and(7,2) (5,?) and(5,3) (55) and (5,1) The equation of a circle in general form is 2:2 +3:2 + 2x 8y +16 2 0. What are the center and radius of the circle? (1 point) center: (1,4), r= 4 center: (1,4) , r = 4 center: (1,4), r=1 center: (1,4) , r =1 \fDetermine whether each sequence below is arithmetic, geometric, or neither. Provide support for your conclusions. sequence 1: 1 7 11 5 2'6'6'2' sequence 2: 1 1 2 4 2'3'9' 27 (4 points) BI U WIN-A large asteroid crashed into a moon of another planet causing several boulders from the moon to be propelled into space toward the planet. Astronomers were able to measure the speed of one of the projectiles. The distance (in feet) that the projectile traveled each second, starting with the first second, was given by the arithmetic progression 17,51,85, 1 19, Find the distance that the projectile traveled in the ninth second. (1 point) 306 ft. 323 ft. 255 ft. 289 ft. Calculate 5'22 for the arithmetic sequence in which 012 = 2.4 and the common difference is d = 3.4. (1 point) 15.4 3 5 36.4 59.4 +1 ! Determine the first four terms of the sequence in which the nth term is at,l = (n ) (n+2)!' (1point) 1111 2'3'4'5 ll 1 l 3'4'5'6 l l l 1 2'2 2'2 3 2 4. 2 3'4'5'6