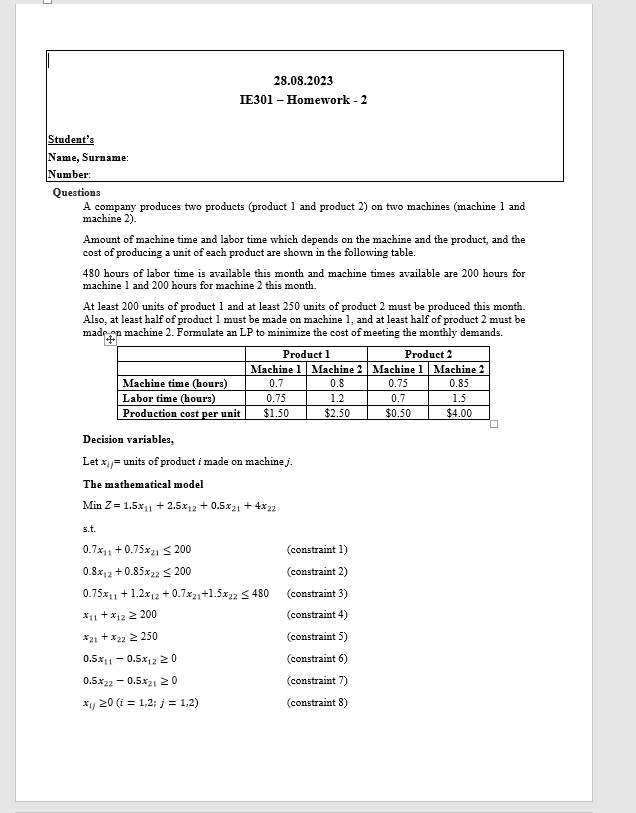
Write the GAMS code of the given mathematical model. Answer the following questions. 1. What are the optimum Z value and decision variable values? (For Z2x11,x12,x21,x22 specify the values separately) 2. Which one(s) of the constraint(s) is(are) binding? Which is(are) non-binding? Why? 3. What are the shadow prices for all constraints? What do they mean for this model? Specify one by one. 4. What are the reduced costs for all variables? What do they mean for the model? Specify one by one. 5. If machine time available were 150 hours for machine 2 , would the current optimal basic solution change? Why? If the current optimal basic solution changes, what are the new values? 6. If labor time available were 380 hours, would the current optimal basic solution change? Why? If the current optimal basic solution changes, what are the new values? 7. If the production cost for machine 1 product 2 were 2.5 , would the current optimal basic solution change? Why? If the current optimal basic solution changes, what are the new values? 8. If demand for product 2 were 300 , would the current optimal basic solution change? Why? If the current optimal basic solution changes, what are the new values? aswers A company produces two products (product 1 and product 2) on two machines (machine 1 and machine 2). Amount of machine time and labor time which depends on the machine and the product, and the cost of producing a unit of each product are shown in the following table. 480 hours of labor time is available this month and machine times available are 200 hours for machine 1 and 200 hours for machine 2 this month. At least 200 units of product 1 and at least 250 units of product 2 must be produced this month. Also, at least half of product 1 must be made on machine 1 , and at least half of product 2 must be madp on machine 2. Formulate an LP to minimize the cost of meeting the monthly demands. Decision variables, Let xij= units of product i made on machine j. The mathematical model MinZ=1.5x11+2.5x12+0.5x21+4x27