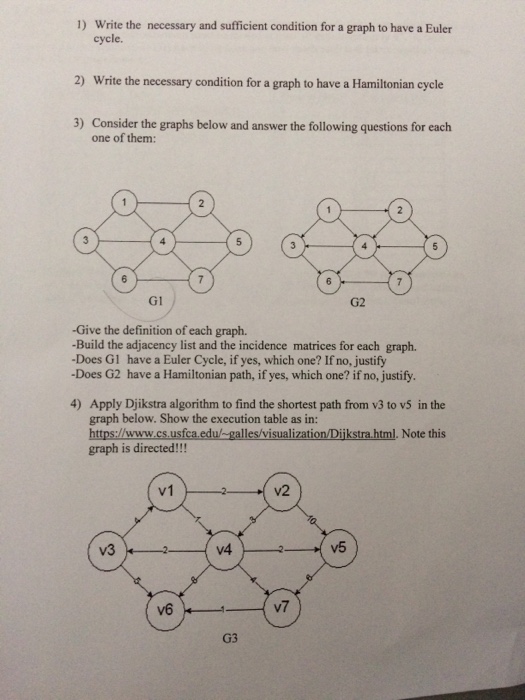
Write the necessary and sufficient condition for a graph to have a Euler cycle. Write the necessary condition for a graph to have a Hamiltonian cycle Consider the graph below and answer the following question for each one of them: Give the definition of each graph. Build the adjacency list and the incidence matrices for each graph. Does G1 have a Euler Cycle, if yes, which one? If no, justify Does G2 have a Hamiltonian path, if yes, which one? If no, justify. Apply Djikstra algorithm to find the shortest path from v3 to v5 in the graph given below. Show the execution table as in: https://www.cs.usfca.edu/-galles/visulization/Dijkstra.html. Note this graph is directed