Write the required functions and script that prompts the user for the name of a file representing a finite automaton: indicating its states and input->state transitions; reads the information in the file (storing the finite automaton in a dictionary); prints the finite-automaton/dictionary in a special form; prompts the user for the name of a file storing the start-state and inputs to process (each line in the file contains this combination); repeatedly processes these lines, computing the results of the finite automaton on each input, and then prints the results. Note that a finite automaton is really a program; in this problem we are reading a program from a file and then executing it (running the finite automaton) on various inputs. So, we are really writing a compiler/interpreter for a small programming language.

A finite automaton (FA) is an machine that is sometimes called a Deterministic Finite Automaton (DFA; see the next problem for an NDFA: a non-deterministic finite automaton). An FA is described by its states and its transitions: each transition for a state specifies an input and what state in the FA that input leads to. We can illustrate an FA as a graph with state labels in circles and edge labels for transitions (see below).

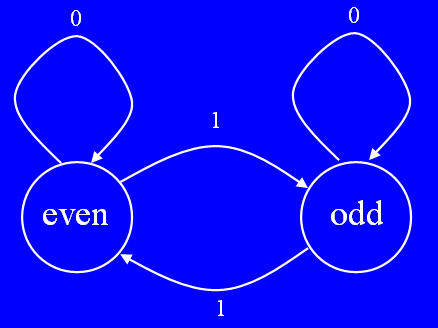
Input and Output:

Read a file that describes a FA: each line contains a state and an arbitrary number of input->state transitions. Build a dictionary such that each key is a str state and whose associated value is another dictionary specifying all the transitions from that state: this second dictionary has keys that are str inputs and associated values are str states. The first token on each line is the str state and the remaining tokens (always coming in pairs) are str inputs and their resulting states. All tokens (which can comprise any number of characters) are separated by one semicolon character. We annotate this dictionary as {str:{str:str}}.

For example, the input file faparity.txt contains the following lines (which could appear in this order, or any other and still specify the same FA):

 even;0;even;1;odd odd;0;odd;1;even

Here is a picture of the parity FA. It graphically illustrates the two states (even and odd) and their transitions, using inputs (0and 1) that always lead back to one of these two states.

Here, the state even (meaning it has seen an even number of 1 inputs so far) is a key in the main dictionary. Its value is a dictionary with two key/value pairs 0->even and 1->odd. It means that in the even state, if the input is a 0 the FA stays in the even state; if the input is a 1 the FA goes to the odd state. And similarly (the next line) means that for the odd state, if the input is a 0 the FA stays in the odd state; if the input is a 1 the FA goes back to the even state. So, seeing an input of 0 keeps the FA in the same state; seeing an input of 1 flips the FA into the other state.

Print the finite automaton, one state (and its transitions) per line; the states are printed alphabetically and the transition dictionary for each state is printed as a list of input/state items (tuples) such that these are printed alphabetically by the inputs.

For example, the file above would print as:

 The Contents of the file picked for this Finite Automaton even transitions: [('0', 'even'), ('1', 'odd')] odd transitions: [('0', 'odd'), ('1', 'even')]

Note that there are multiple data files for this program: faparity.txt and fadivisibleby3.txt; test/debug your program on the first file; when you are done, test it on the last file. Draw the FA represented by each for to ensure that your code correctly prints and computes with it. Important: This task is not to write a Python code that simulates the Parity FA; it is to write code that simulates any FA, whose description it reads from a file.

Next, repeatedly read and process lines from a second input file, computing the results of the finite automaton running on the specified start-state with its inputs; then print out the results in a special form. Each line in the file contains a start-state followed by a sequence of inputs (all separated by semicolons). The start-state will be a state in the FA (it is a key in the outer dictionary) the inputs may specify legal or illegal transitions (may or may not be keys in some inner dictonary).

For example, the input file fainputparity.txt contains the following three lines:

 even;1;0;1;1;0;1 even;1;0;1;1;0;x odd;1;0;1;1;0;1

The first line means, the start-state is even and the inputs are 1, 0, 1, 1, 0, and 1.

The result of processing each line is to print the start-state, and then each input and the new state it transitions to, and finally print the stop-state. For the parity FA and the first line in this file, it should print

Start state = even Input = 1; new state = odd Input = 0; new state = odd Input = 1; new state = even Input = 1; new state = odd Input = 0; new state = odd Input = 1; new state = even Stop state = even

Note that the second line contains an input x which is not a legal input allowed in any state; any such input should stop the simulation for that line only, continuing to start a new simulation for all following lines (as illustrated in the Sample Interaction).

Functions and Script:

Write the following functions and script. I am providing line counts for these function bodies not as requirements, but to indicate the lengths of well-written Pythonic code.

• read_fa has an open (file) parameter; it returns the dictionary representing the finite automaton; hint: I used splicing and the zip function to build the inner dictionaries. (body is 6 lines).

• fa_as_str has a dictionary parameter (representing the FA); it returns a multi-line string (each line is ended by ' '), which when printed shows the contents of the FA in the appropriate textual form: sorted alphabetically by state, with a state's transitions sorted by their input value (body is 4 lines; can you do it in 1?).

• process has a dictionary parameter (representing the FA), a str parameter (representing the start-state), and a list parameter (representing a list of str inputs); it returns a list that contains the start-state followed by tuples that show the input and resulting state after each transition. For the example shown above, process returns the following list.

  ['even', ('1', 'odd'), ('0', 'odd'), ('1', 'even'), ('1', 'odd'), ('0', 'odd'), ('1', 'even')]

  Finally, if an input is illegal (is not the key in some transition for the current state), say 'x', for the parity FA, then processshould terminate with the last tuple in the list indicating a problem: ('x', None) (body is 9 lines).

• interpret has a list parameter (the list result produced by process); it returns a multi-line string (each line is ended by ' '), which when printed illustrates the results of processing an FA on an input in the appropriate textual form. See how it prints the example list argument shown above in the output further above. Also see the Sample Interaction below to see how it prints input errors: see the middle example (body is 9 lines).

• Write a script at the bottom of this module (in if __name__ == '__main__':) that prompts the user to enter the file describing the FA, prints it, prompts the user to enter the file containing lines of start-states and input, simulates the FA on each line, printing the results in the appropriate textual form (body is 7 lines).

Sample Interaction:

The program, as specified, will have the following interaction: user-typed information appears in italics. Your output should match this one.

 Pick the file name containing this Finite Automaton: faparity.txt The Contents of the file picked for this Finite Automaton even transitions: [('0', 'even'), ('1', 'odd')] odd transitions: [('0', 'odd'), ('1', 'even')] Pick the file name containing a sequence of start-states and subsequent inputs: fainputparity.txt Commence tracing this FA from its start-state Start state = even Input = 1; new state = odd Input = 0; new state = odd Input = 1; new state = even Input = 1; new state = odd Input = 0; new state = odd Input = 1; new state = even Stop state = even Commence tracing this FA from its start-state Start state = even Input = 1; new state = odd Input = 0; new state = odd Input = 1; new state = even Input = 1; new state = odd Input = 0; new state = odd Input = x; illegal input: simulation terminated Stop state = None Commence tracing this FA from its start-state Start state = odd Input = 1; new state = even Input = 0; new state = even Input = 1; new state = odd Input = 1; new state = even Input = 0; new state = even Input = 1; new state = odd Stop state = odd

You can also try the fadivisibleby3.txt finite automaton file, which determines whether an integer (sequence of digits) is divisible by 3: it is divisible if the finite automaton stops in state rem0. It's input file fainputdivisibleby3.txt tries the number12,435,711, which is divisible by 3 and number 823, which is not divisible by 3: dividing 823 by 3 leaves a remainder of 1.

even odd even odd