Write this program in C or C++

Output:

Lagrange Interpolation function

Parameters:

n order of polynomial+1

x - where to evaluate xk[n]

x_values fk[n]

Y_value(true value)

double lagrange (int n, double x, double* xk, double* fk) {

int i, k;

double p, lk;

p = 0.0;

for (k=0; k

lk = 1.0;

for (i=0; i

if (i==k)

continue;

/* accumulate Lk(x) */

lk *= (x - xk[i])/(xk[k] - xk[i]); }

/* accumulate the sum */

p += lk*fk[k]; } r

eturn p; }

//To call your function:

for (k=0; k

xk = y[k];

p = lagrange (order+1 , xk, x, f);

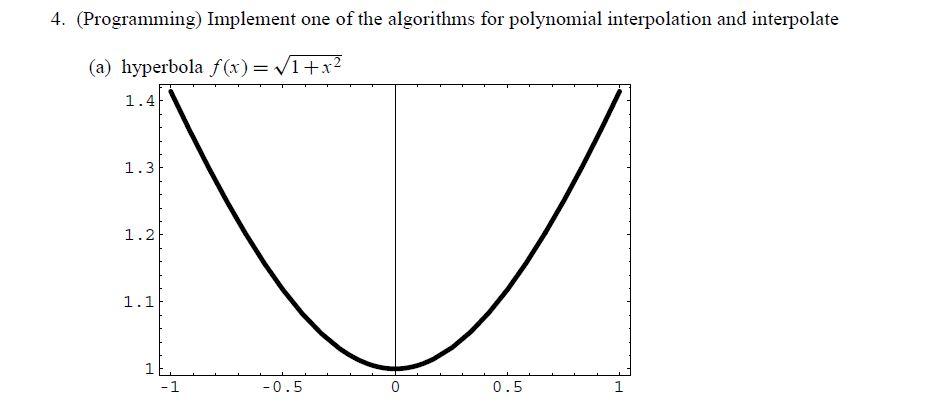
4. (Programming) Implement one of the algorithms for polynomial interpolation and interpolate (a) hyperbola f(x)= (1+x2 1.4 1.3 1.2 1.1 1 -1 -0.5 O 0.5 1 (b) Runge's function f(x) = 1+25x2 1 0.8 0.6 u 0.4 0.2 0 -1 -0.5 0 0.5 1 using a set of n +1 regularly spaced nodes 2 (k-1) Xk=-1+ ) k=1,2,....n+1. 72 Test your generated polynomial with different orders, n= 5, 10, 20 and compute the interpolation polynomial Pn(x) at 41 regularly spaced points. For each value of xk the Lagrange polynomial approximation is output together with the exact /true value from the math library, also output the absolute error. Example Output: Lagrange interpolation MENU 1. Function A 2. Function 3. Quit Enter your choice: 1 WHEN 5 K Xk 0 1 2 3 4 5 6 7 P -1.0000000 1.4142140 -0.9500000 1.3802810 -0.9000000 1.3468090 -0.8500000 1.3139990 -0.8000000 1.2820420 -0.7500000 1.2511190 -0.7000000 1.2213990 -0.6500000 1.1930400 -0.6000000 1.1661900 -0.5500000 1.1409860 -0.5000000 1.1175530 -0.4500000 1.0960050 -0.4000000 1.0764470 -0.3500000 1.0589710 -0.3000000 1.0436600 .2500000 1.0305840 -0.2000000 1.0198040 TRUE VALUE 1.414213562 1.379311422 1.345362405 1.312440475 1.280624847 1.25 1.220655562 1.192686044 1.166190379 1.141271221 1.118033989 1.09658561 1.077032961 1.059481005 1.044030651 1.030776406 1.019803903 ABSOLUTE ERROR 4.38E-07 9.70E-04 1.45E-03 1.56E-03 1.42E-03 1.12E-03 7.43E-04 3.54E-04 3.79E-07 2.85E-04 4.81E-04 5.81E-04 5.86E-04 5.10E-04 3.71E-04 1.92E-04 9.73E-08 8 9 10 11 12 13 14 15 16 2 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 -0.1500000 1.0113680 -0.1000000 1.0053150 -0.0500000 1.0016730 0.0000000 1.0004570 0.0500000 1.0016730 0.1000000 1.0053150 0.1500000 1.0113680 0.2000000 1.0198040 0.2500000 1.0305840 0.3000000 1.0436600 0.3500000 1.0589710 0.4000000 1.0764470 0.4500000 1.0960050 0.5000000 1.1175530 0.5500000 1.1409860 0.6000000 1.1661900 0.6500000 1.1930400 0.7000000 1.2213990 0.7500000 1.2511190 0.8000000 1.2820420 0.8500000 1.3139990 0.9000000 1.3468090 0.9500000 1.3802810 1.0000000 1.4142140 1.011187421 1.004987562 1.00124922 1 1.00124922 1.004987562 1.011187421 1.019803903 1.030776406 1.044030651 1.059481005 1.077032961 1.09658561 1.118033989 1.141271221 1.166190379 1.192686044 1.220655562 1.25 1.280624847 1.312440475 1.345362405 1.379311422 1.414213562 1.81E-04 3.27E-04 4.24E-04 4.57E-04 4.24E-04 3.27E-04 1.81E-04 9.73E-08 1.92E-04 3.71E-04 5.10E-04 5.86E-04 5.81E-04 4.81E-04 2.85E-04 3.79E-07 3.54E-04 7.43E-04 1.12E-03 1.42E-03 1.56E-03 1.45E-03 9.70E-04 4.38E-07 WHEN n-10 .....display 41 column table....... WHEN n=15 ..........display 41 column table ........ MENU 1. Function A 2. Function B 3. Quit Enter your choice: 2 WHEN n 5 ......display 41 column table WHEN n=10 3 ...display 41 column table ........ WHEN 1=15 ......display 41 column table MENO 1. Function A 2. Function B 3. Quit Enter your choice: 3 Exit 4 4. (Programming) Implement one of the algorithms for polynomial interpolation and interpolate (a) hyperbola f(x)= (1+x2 1.4 1.3 1.2 1.1 1 -1 -0.5 O 0.5 1 (b) Runge's function f(x) = 1+25x2 1 0.8 0.6 u 0.4 0.2 0 -1 -0.5 0 0.5 1 using a set of n +1 regularly spaced nodes 2 (k-1) Xk=-1+ ) k=1,2,....n+1. 72 Test your generated polynomial with different orders, n= 5, 10, 20 and compute the interpolation polynomial Pn(x) at 41 regularly spaced points. For each value of xk the Lagrange polynomial approximation is output together with the exact /true value from the math library, also output the absolute error. Example Output: Lagrange interpolation MENU 1. Function A 2. Function 3. Quit Enter your choice: 1 WHEN 5 K Xk 0 1 2 3 4 5 6 7 P -1.0000000 1.4142140 -0.9500000 1.3802810 -0.9000000 1.3468090 -0.8500000 1.3139990 -0.8000000 1.2820420 -0.7500000 1.2511190 -0.7000000 1.2213990 -0.6500000 1.1930400 -0.6000000 1.1661900 -0.5500000 1.1409860 -0.5000000 1.1175530 -0.4500000 1.0960050 -0.4000000 1.0764470 -0.3500000 1.0589710 -0.3000000 1.0436600 .2500000 1.0305840 -0.2000000 1.0198040 TRUE VALUE 1.414213562 1.379311422 1.345362405 1.312440475 1.280624847 1.25 1.220655562 1.192686044 1.166190379 1.141271221 1.118033989 1.09658561 1.077032961 1.059481005 1.044030651 1.030776406 1.019803903 ABSOLUTE ERROR 4.38E-07 9.70E-04 1.45E-03 1.56E-03 1.42E-03 1.12E-03 7.43E-04 3.54E-04 3.79E-07 2.85E-04 4.81E-04 5.81E-04 5.86E-04 5.10E-04 3.71E-04 1.92E-04 9.73E-08 8 9 10 11 12 13 14 15 16 2 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 -0.1500000 1.0113680 -0.1000000 1.0053150 -0.0500000 1.0016730 0.0000000 1.0004570 0.0500000 1.0016730 0.1000000 1.0053150 0.1500000 1.0113680 0.2000000 1.0198040 0.2500000 1.0305840 0.3000000 1.0436600 0.3500000 1.0589710 0.4000000 1.0764470 0.4500000 1.0960050 0.5000000 1.1175530 0.5500000 1.1409860 0.6000000 1.1661900 0.6500000 1.1930400 0.7000000 1.2213990 0.7500000 1.2511190 0.8000000 1.2820420 0.8500000 1.3139990 0.9000000 1.3468090 0.9500000 1.3802810 1.0000000 1.4142140 1.011187421 1.004987562 1.00124922 1 1.00124922 1.004987562 1.011187421 1.019803903 1.030776406 1.044030651 1.059481005 1.077032961 1.09658561 1.118033989 1.141271221 1.166190379 1.192686044 1.220655562 1.25 1.280624847 1.312440475 1.345362405 1.379311422 1.414213562 1.81E-04 3.27E-04 4.24E-04 4.57E-04 4.24E-04 3.27E-04 1.81E-04 9.73E-08 1.92E-04 3.71E-04 5.10E-04 5.86E-04 5.81E-04 4.81E-04 2.85E-04 3.79E-07 3.54E-04 7.43E-04 1.12E-03 1.42E-03 1.56E-03 1.45E-03 9.70E-04 4.38E-07 WHEN n-10 .....display 41 column table....... WHEN n=15 ..........display 41 column table ........ MENU 1. Function A 2. Function B 3. Quit Enter your choice: 2 WHEN n 5 ......display 41 column table WHEN n=10 3 ...display 41 column table ........ WHEN 1=15 ......display 41 column table MENO 1. Function A 2. Function B 3. Quit Enter your choice: 3 Exit 4