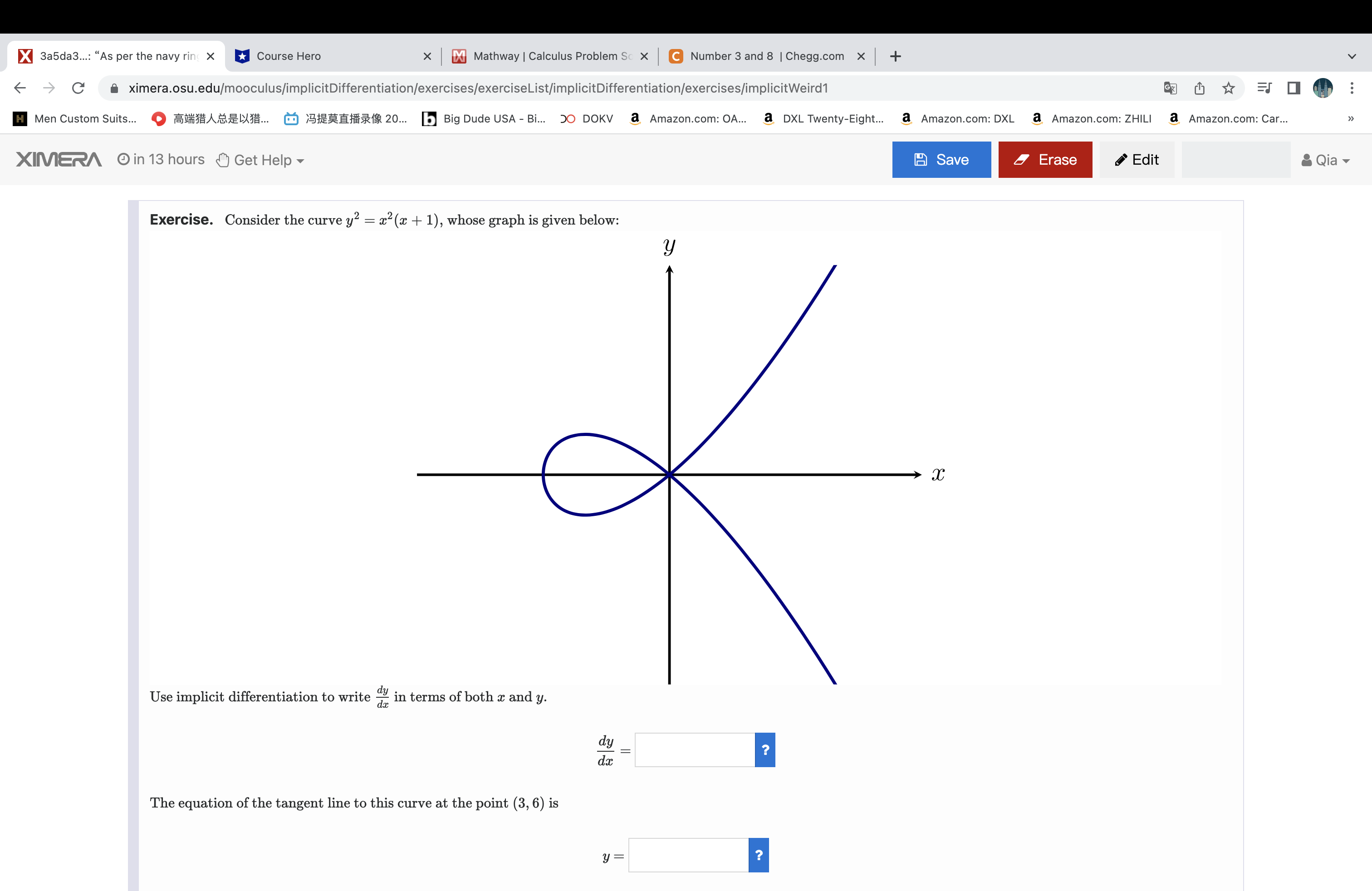
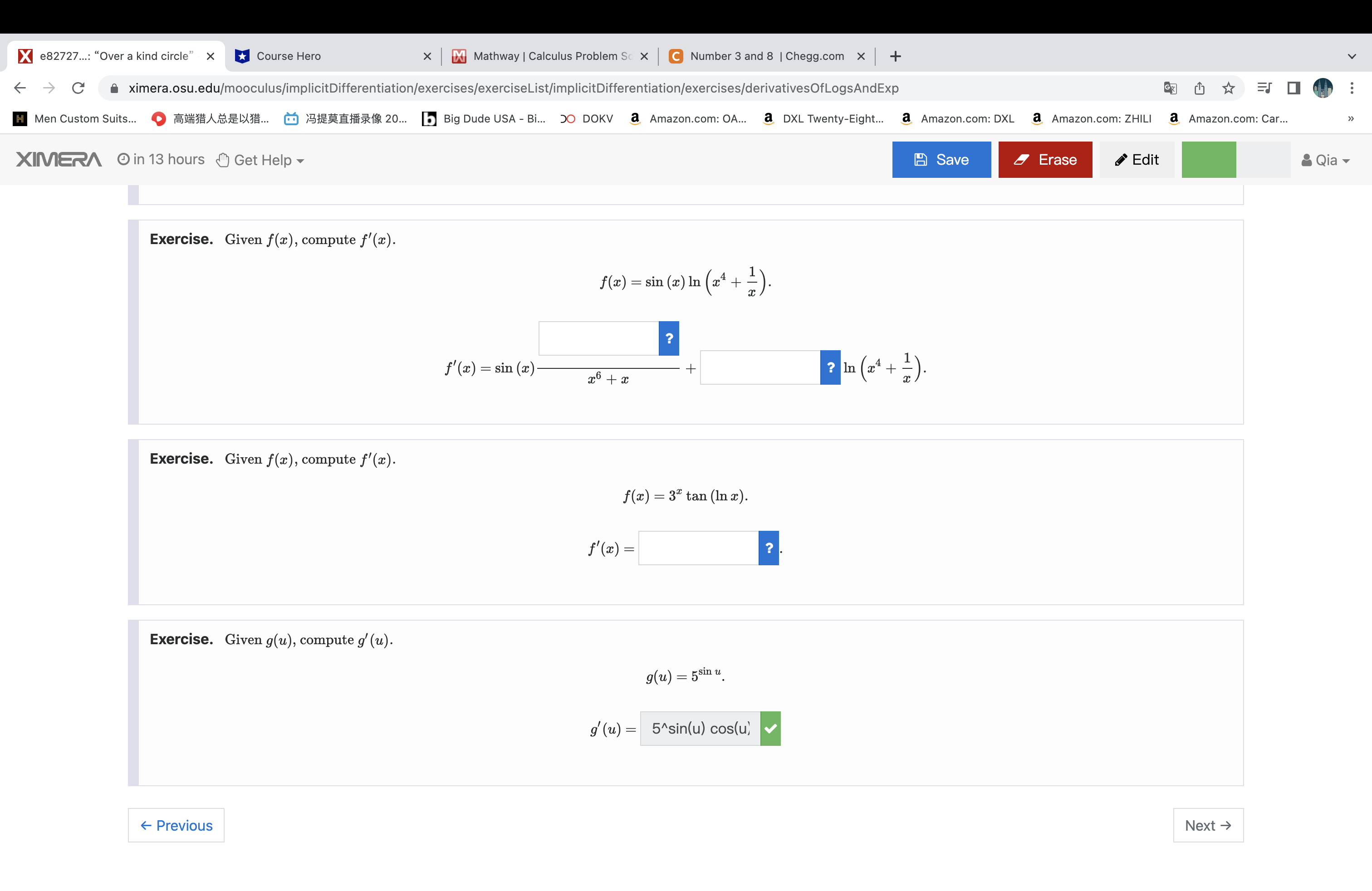
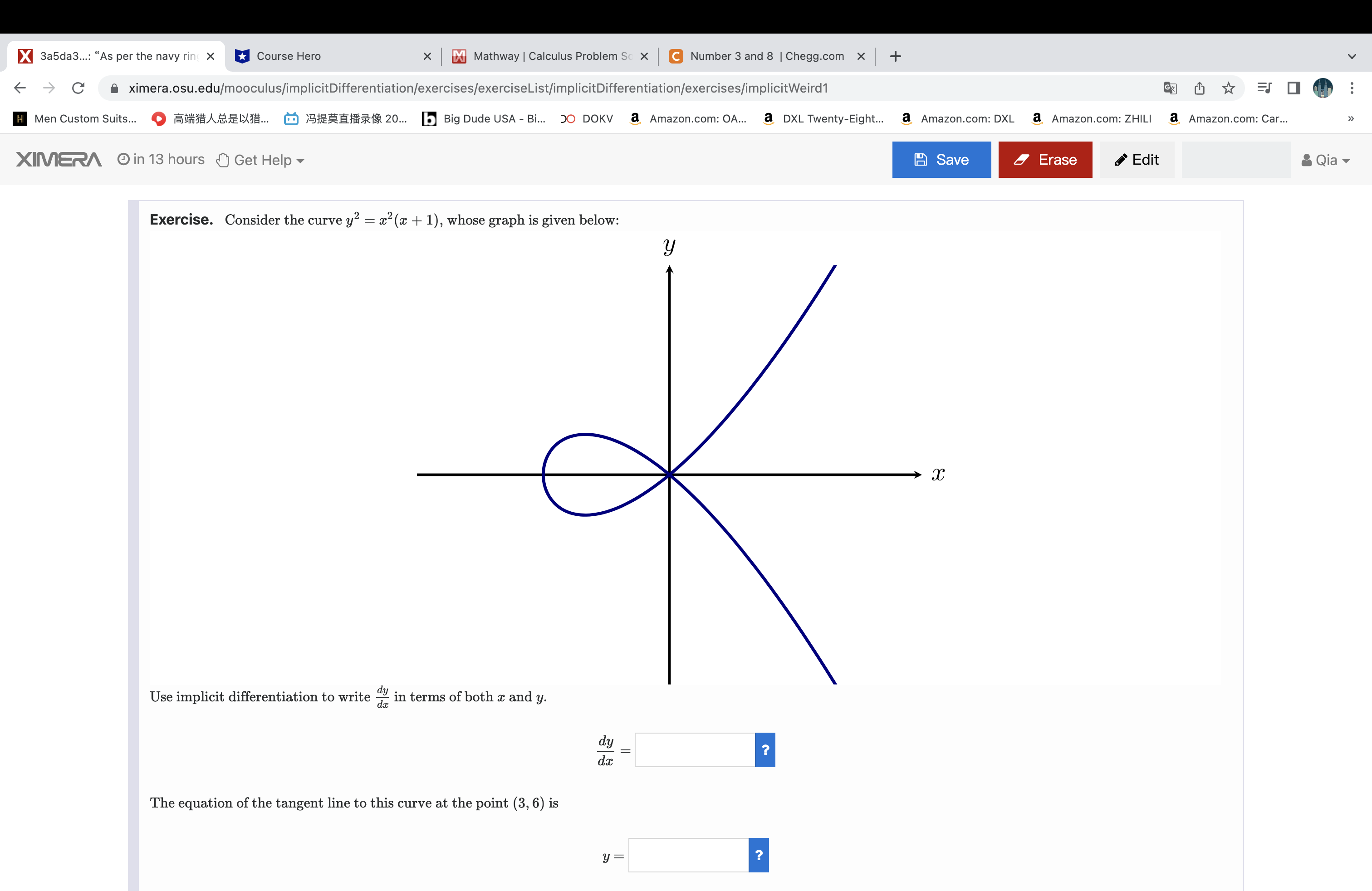
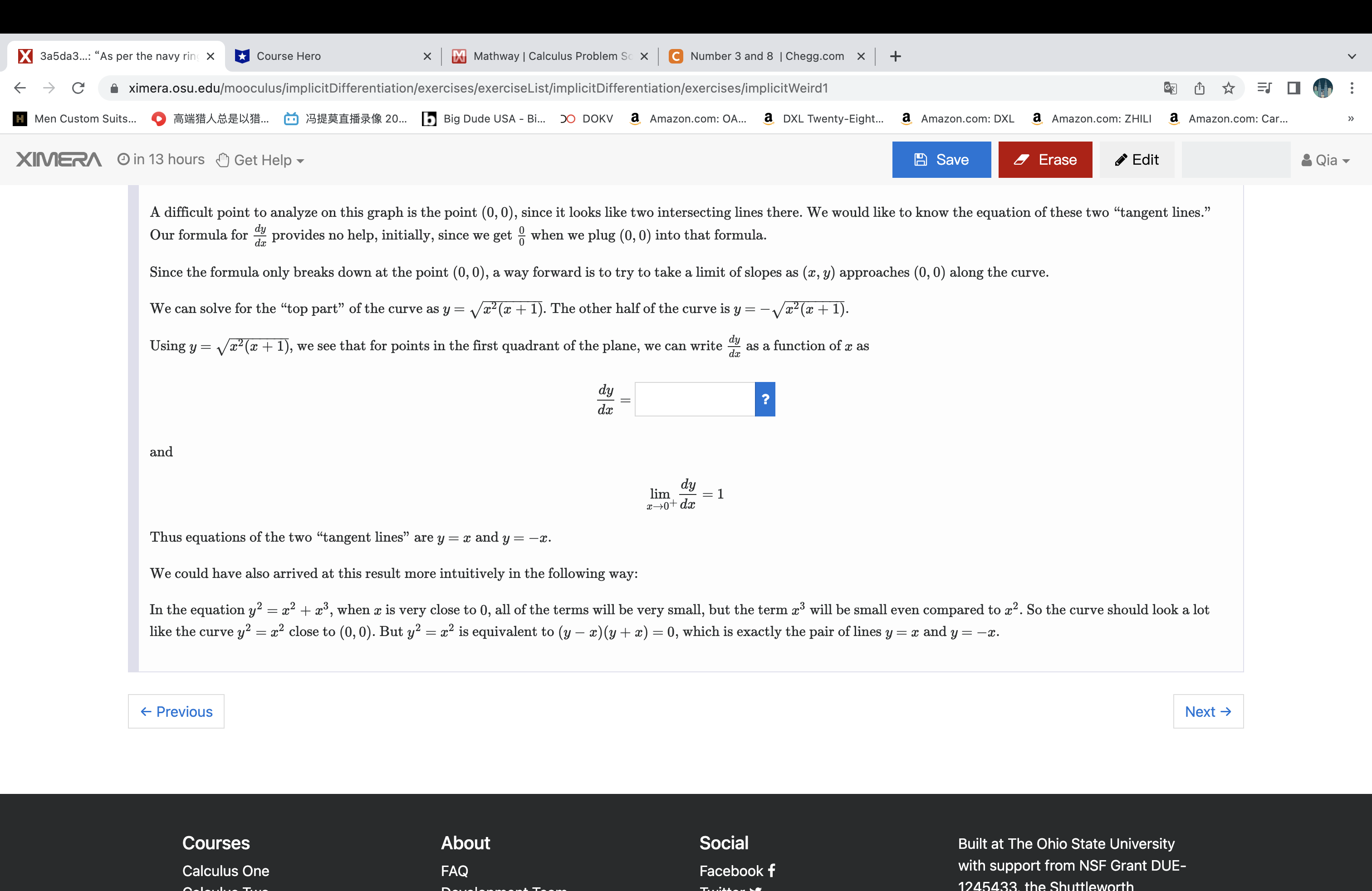
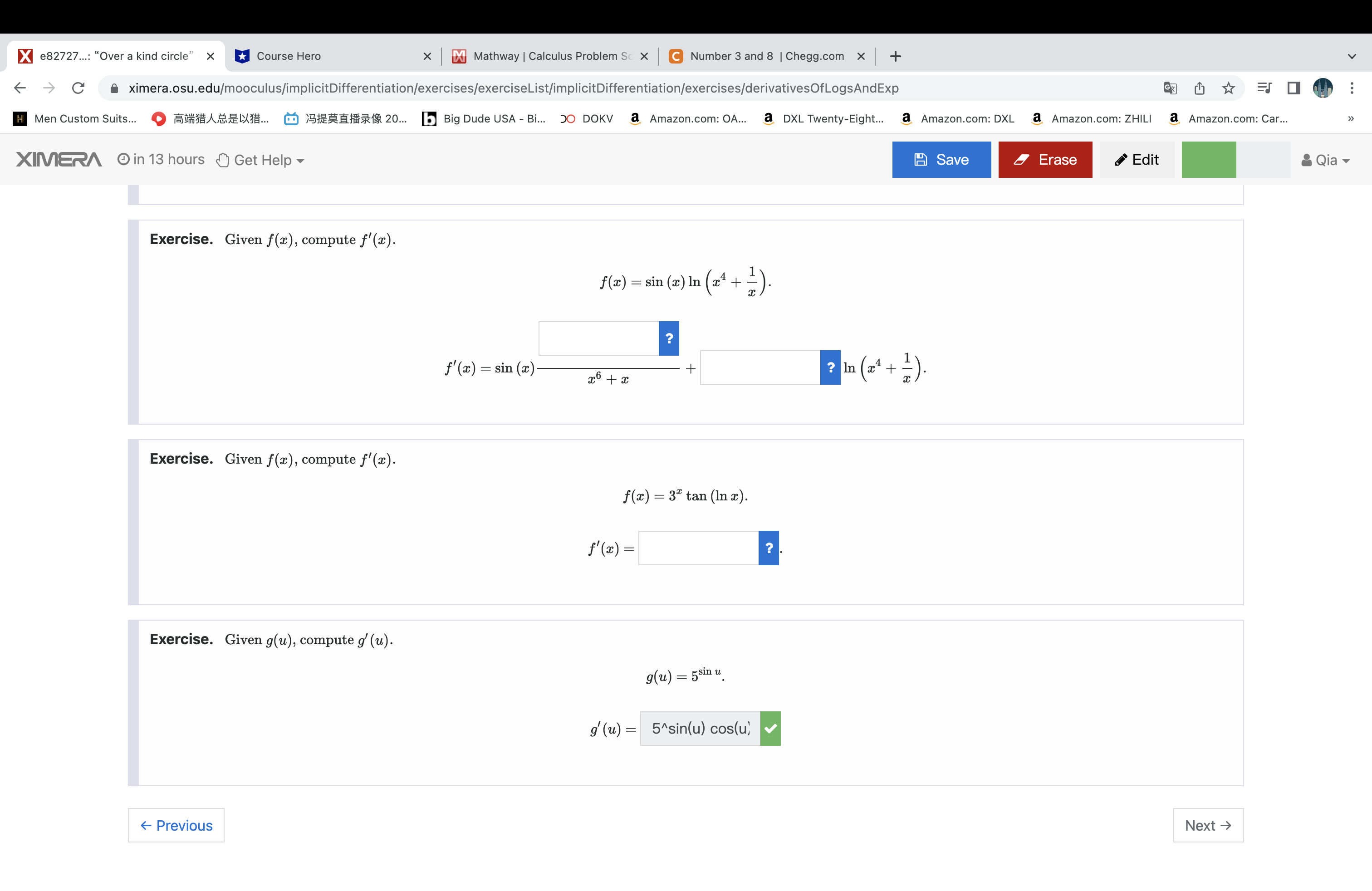
X 3a5da3...: "As per the navy ring X Course Hero x Mathway | Calculus Problem Sc X C Number 3 and 8 | Chegg.com x + -> C ximera.osu.edu/mooculus/implicitDifferentiation/exercises/exerciseList/implicitDifferentiation/exercises/implicitWeird1 GZ H Men Custom Suits... O BASEXX... O SHERHAS 20... b Big Dude USA - Bi... 50 DOKV a Amazon.com: OA... a DXL Twenty-Eight... a Amazon.com: DXL a Amazon.com: ZHILI a Amazon.com: Car... XIMERA in 13 hours Get Help Save Erase Edit Qia Exercise. Consider the curve y? = x2(x + 1), whose graph is given below: y Use implicit differentiation to write an in terms of both x and y. dy dx The equation of the tangent line to this curve at the point (3, 6) is y =X 3a5da3...: "As per the navy ring X Course Hero x Mathway | Calculus Problem Sc X C Number 3 and 8 | Chegg.com x + -> C ximera.osu.edu/mooculus/implicitDifferentiation/exercises/exerciseList/implicitDifferentiation/exercises/implicitWeird1 GZ chy H Men Custom Suits... O BABE.. 0 9:26218 20... b Big Dude USA - Bi... 50 DOKV a Amazon.com: OA... a DXL Twenty-Eight... a Amazon.com: DXL a Amazon.com: ZHILI a Amazon.com: Car... XINERA in 13 hours Get Help Save Erase Edit Qia A difficult point to analyze on this graph is the point (0, 0), since it looks like two intersecting lines there. We would like to know the equation of these two "tangent lines." Our formula for dy p provides no help, initially, since we get , when we plug (0, 0) into that formula. Since the formula only breaks down at the point (0, 0), a way forward is to try to take a limit of slopes as (x, y) approaches (0, 0) along the curve. We can solve for the "top part" of the curve as y = vx2(x + 1). The other half of the curve is y = - Va(x + 1). Using y = vx2(x + 1), we see that for points in the first quadrant of the plane, we can write - as a function of x as dy da and lim dy - 1 x + dx Thus equations of the two "tangent lines" are y = x and y = -x. We could have also arrived at this result more intuitively in the following way: In the equation y? = x2 + x', when a is very close to 0, all of the terms will be very small, but the term c' will be small even compared to x2. So the curve should look a lot like the curve y? = x2 close to (0, 0). But y2 = x2 is equivalent to (y - x)(y + x) = 0, which is exactly the pair of lines y = x and y = -x. - Previous Next -> Courses About Social Built at The Ohio State University Calculus One FAQ Facebook f with support from NSF Grant DUE- 1245433 +X e82727...: "Over a kind circle" x Course Hero x Mathway | Calculus Problem Sc X C Number 3 and 8 | Chegg.com x + - C ximera.osu.edu/mooculus/implicitDifferentiation/exercises/exerciseList/implicitDifferentiation/exercises/derivativesOfLogsAndExp H Men Custom Suits... OSHASEX... @ SHEHAS 20... b Big Dude USA - Bi... 50 DOKV a Amazon.com: OA... a DXL Twenty-Eight... a Amazon.com: DXL a Amazon.com: ZHILI a Amazon.com: Car... XIMERA in 13 hours Get Help Save Erase Edit Qia Exercise. Given f(x), compute f'(x). f (x) = sin (x) In (24 + = ). f'(x) = sin (ac) + ? In ( 2 4 + 2 ) Exercise. Given f(x), compute f'(x). f (2) = 32 tan (In x). f' (20 ) = Exercise. Given g(u), compute g' (u). g(u) = 5sin u g' (u) = 5^sin(u) cos(u) Previous Next >