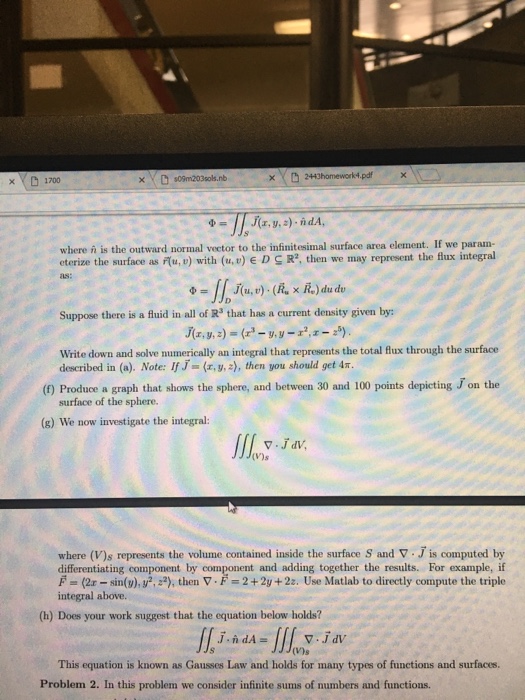
x CD 2413homework4pdf x Problem 1. This problem deals with integration over a parametrized surface. (a) Parameterize the sphere of radius one centered at the origin. Write your parameterization nicely using an equation editor in your document. Plot the surface in 3D. (b) Write down a double integral that represents the surface area the surface in (a). Compute the surface area using Matlab. Check your answer using known formula. (c) write down a triple integral that represents the volume enclosed by the surface in (a). Compute the volume using Matlab. Check your answer using known formula. (d) suppose there is a fluid inside the sphere with density given by p(r,y,z) erv- va. write down triple integrals that represent the spheres mass, and center of mass (in each coordinate Use Matlab to generate approxim ations of each. Note: If p(a, y, z) 1 you can do this by hand and intuition to check if your code works. (e) Given a current density J flux 4 of J through a surface S is given by Ja, Jv, J.), the where is the outward normal vector to the infinitesimal surface area element. If we param eterize the surface i(u, v) with D we may represent the flux integral as suppose there is a fluid in all of R3 that has a current density given by: write down and solve numerically an integral that represents the total flux through the surface described in (a. Note: If J (r, y, z), then you should get im. (f Produce a graph that shows the sphere, and between 30 and 100 points depicting j on the surface of the sphere. v. J dv, where (V)s represents the volume contained inside the surface s and v J is computed by differentiating component by component and adding together the results. For example, if F w 2a sin(v), v?,z?), then v. F 2 +2y 22. Use Matlab to directly compute the triple integral above. (b) Does your work suggest that the equation below holds